Page 166 - Electric Drives and Electromechanical Systems

Chapter 5 Brushed direct-current motors 159

On solving for E r , it is possible to determine that the total regenerative energy that is
returned to the drive when a rotating system is decelerated from u int , to standstill is,
t
Z 0 2
R
u int K e t 0 u int K e þ I R a
E r ¼ t u int K e þ I R R a I R dt ¼ (5.27)
t z 2
0
The above equations express the regeneration energy in terms of the time for the
motor’s terminal voltage to reach zero. The total time for the system to reach zero speed
can be determined from the deceleration torque, T d , and the system inertia, I tot , using,
u int
a ¼ (5.28)
t z
I tot u int
K t I R ¼ T d ¼ I tot a ¼ (5.29)
t z
Hence it is possible to determine that
2 2
I tot u int u int K e I R a
R
E r ¼ þ þ I R R a (5.30)
K t 2 2u int K e
The first two terms in the parentheses of Eq. (5.30) are positive and represent the
energy dissipation outside the motor, while the third term is negative and represents the
energy dissipated in the armature resistance (as the regenerative current, I R is negative).
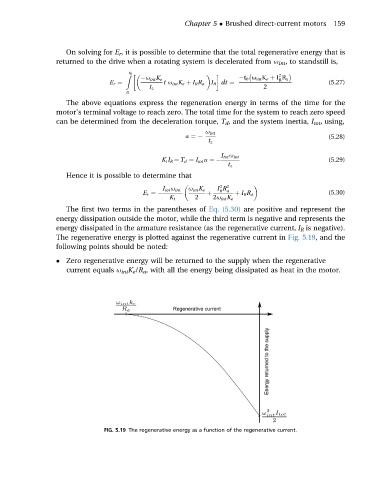
The regenerative energy is plotted against the regenerative current in Fig. 5.19, and the
following points should be noted:

Zero regenerative energy will be returned to the supply when the regenerative
current equals u int K e /R a , with all the energy being dissipated as heat in the motor.

FIG. 5.19 The regenerative energy as a function of the regenerative current.