Page 261 - Elements of Chemical Reaction Engineering 3rd Edition

Sec. 5.1 Batch Reactor Data 233

Polynomial (POLYMATH). Another method to determine dPldt is to fit the total
pressure to a polynomial in time and then to differentiate the resulting polynomial.
Choosing a fourth-order polynomial
P = a, + a,t + a2t2 + a,t3 + a,t4 (Ec5-1.8)
we use the POLYMATH software package to express pressure as a function of time.
Here we first choose the polynomial order (in this case fourth order) and then type
in the values of P at various times t to obtain
P(t) = 7.53 + 2.31t- 0.0718t2 + 0.00276t3 - 4.83 X lOP5t4 (E15-1.9)
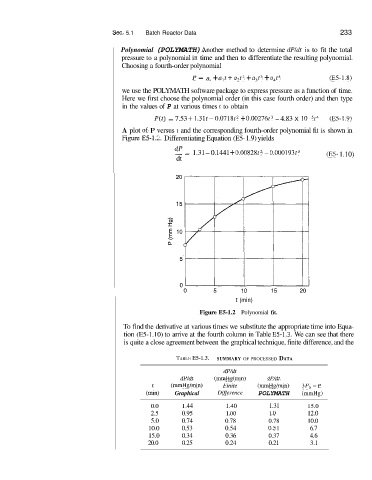
A plot of P versus t and the corresponding fourth-order polynomial fit is shown in
Fipre E5-1.L. Differentiating Equation (E5- 1.9) yields

dP -- 1.31 - 0.1441 + 0.00828t2 - 0.000193t3 (E5- 1.10)
-
dt

t (min)

Figure E5-1.2 Polynomial fit.
To find the derivative at various times we substitute the appropriate time into Equa-
tion (E5-1.10) to arrive at the fourth column in Table E5-1.3. We can see that there
is quite a close agreement between the graphical technique, finite difference, and the
TABLE E5-1.3. SUMMARY OF PROCESSED DATA

dP/dt
dP/dt (mmHglmin) dP/dt
t (mmHg/mn) Finite (mmHg/min) 3P, - P
(rmn) Graphical Dzfleer-ence POLYMATH (mmHg)
0.0 I .44 1.40 1.31 15.0
2.5 0.95 1 .oo 1 .o 12.0
5.0 0.74 0.78 0.78 10.0
10.0 0.53 0.54 0.5 1 6.7
15.0 0.34 0.36 0.37 4.6
20.0 0.25 0.24 0.21 3.1