Page 277 - Academic Press Encyclopedia of Physical Science and Technology 3rd Chemical Engineering

P1: GLM/GLT P2: GLM Final
Encyclopedia of Physical Science and Technology En006G-249 June 27, 2001 14:7

Fluid Dynamics (Chemical Engineering) 69

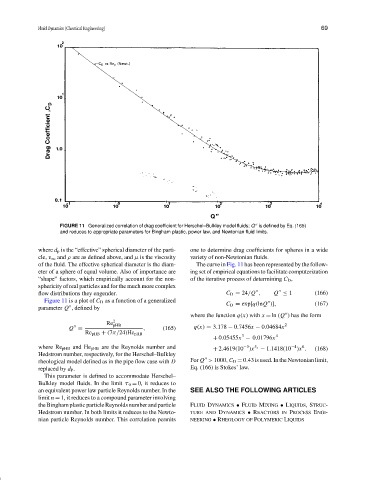
FIGURE 11 Generalized correlation of drag coefficient for Herschel–Bulkley model fluids; Q is defined by Eq. (165)

and reduces to appropriate parameters for Bingham plastic, power law, and Newtonian fluid limits.

where d p is the “effective” spherical diameter of the parti- one to determine drag coefficients for spheres in a wide
cle, v ∞ and ρ are as defined above, and µ is the viscosity variety of non-Newtonian fluids.
of the fluid. The effective spherical diameter is the diam- The curve in Fig. 11 has been represented by the follow-
eter of a sphere of equal volume. Also of importance are ing set of empirical equations to facilitate computerization
“shape” factors, which empirically account for the non- of the iterative process of determining C D ,
sphericity of real particles and for the much more complex

flow distributions they engender. C D = 24/Q , Q ≤ 1 (166)
Figure 11 is a plot of C D as a function of a generalized
C D = exp[q(lnQ )], (167)

parameter Q ,defined by

where the function q(x) with x = ln (Q ) has the form
Re 2 2
pHB q(x) = 3.178 − 0.7456x − 0.04684x
Q = , (165)
Re pHB + (7π/24)He pHB 3 4
+ 0.05455x − 0.01796x
−4
−3
where Re pHB and He pHB are the Reynolds number and + 2.4619(10 )x 5 x − 1.1418(10 )x . (168)
6
Hedstrom number, respectively, for the Herschel–Bulkley

rheological model defined as in the pipe flow case with D For Q > 1000, C D = 0.43 is used. In the Newtonian limit,
replaced by d P . Eq. (166) is Stokes’ law.
This parameter is defined to accommodate Herschel–
Bulkley model fluids. In the limit τ 0 = 0, it reduces to
an equivalent power law particle Reynolds number. In the SEE ALSO THE FOLLOWING ARTICLES
limit n = 1, it reduces to a compound parameter involving
theBinghamplasticparticleReynoldsnumberandparticle FLUID DYNAMICS • FLUID MIXING • LIQUIDS,STRUC-
Hedstrom number. In both limits it reduces to the Newto- TURE AND DYNAMICS • REACTORS IN PROCESS ENGI-
nian particle Reynolds number. This correlation permits NEERING • RHEOLOGY OF POLYMERIC LIQUIDS