Page 196 - Academic Press Encyclopedia of Physical Science and Technology 3rd Polymer

P1: GLM Final Pages
Encyclopedia of Physical Science and Technology EN012c-598 July 26, 2001 15:59

Polymers, Mechanical Behavior 705

speeds. Due to the poor thermal conductivity of the poly- implies how the material will change in volume in ten-
meric tire, the rise in temperature of the internal part of sile deformation. (The volume does not change in simple
the tire can be considerable, and in fact severe degrada- shear.) In brief, for an incompressible constant-volume
tion would rapidly develop were it not for the appropri- deformation behavior, µ equals 0.5, whereas for all other
ate chemical stabilizer package added during rubber com- isotropic systems, µ is less than 0.5 and usually ranges
pounding. Although hysteresis may be viewed somewhat between 0.3 and 0.4 for glassy and semicrystalline poly-
as a disadvantage in some cases (i.e., generation of heat), meric materials. For elastomers, however, µ may indeed
it may also serve a useful role in helping to “dampen out” approach 0.5 and be as high as 0.496. An important point
the transfer of energy in systems undergoing cyclic load- to recognize is that as µ becomes less than 0.5, tensile
ing. For example, such damping materials might be uti- deformation of the material will cause an increase in vol-
lizedasvibrationalmounts.Indeed,recognitionofthehys- ume. At small deformation, this change in volume can be
teresis properties of materials is very important in many written
applications.
V/V 0 = (1 − 2µ)ε. (17)
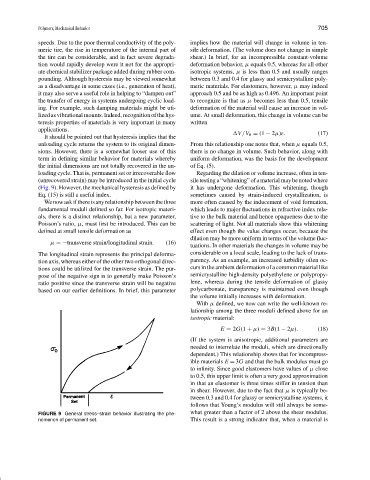
It should be pointed out that hysteresis implies that the
unloading cycle returns the system to its original dimen- From this relationship one notes that, when µ equals 0.5,
sions. However, there is a somewhat looser use of this there is no change in volume. Such behavior, along with
term in defining similar behavior for materials whereby uniform deformation, was the basis for the development
the initial dimensions are not totally recovered in the un- of Eq. (5).
loading cycle. That is, permanent set or irrecoverable flow Regarding the dilation or volume increase, often in ten-
(unrecovered strain) may be introduced in the initial cycle sile testing a “whitening” of a material may be noted where
(Fig. 9). However, the mechanical hysteresis as defined by it has undergone deformation. This whitening, though
Eq. (15) is still a useful index. sometimes caused by strain-induced crystallization, is
Wenowaskifthereisanyrelationshipbetweenthethree more often caused by the inducement of void formation,
fundamental moduli defined so far. For isotropic materi- which leads to major fluctuations in refractive index rela-
als, there is a distinct relationship, but a new parameter, tive to the bulk material and hence opaqueness due to the
Poisson’s ratio, µ, must first be introduced. This can be scattering of light. Not all materials show this whitening
defined at small tensile deformation as effect even though the value changes occur, because the
dilation may be more uniform in terms of the volume fluc-
µ =−transverse strain/longitudinal strain. (16)
tuations. In other materials the changes in volume may be
The longitudinal strain represents the principal deforma- considerable on a local scale, leading to the lack of trans-
tion axis, whereas either of the other two orthogonal direc- parency. As an example, an increased turbidity often oc-
tions could be utilized for the transverse strain. The pur- curs in the ambient deformation of a common material like
pose of the negative sign is to generally make Poisson’s semicrystalline high-density polyethylene or polypropy-
ratio positive since the transverse strain will be negative lene, whereas during the tensile deformation of glassy
based on our earlier definitions. In brief, this parameter polycarbonate, transparency is maintained even though
the volume initially increases with deformation.
With µ defined, we now can write the well-known re-
lationship among the three moduli defined above for an
isotropic material:

E = 2G(1 + µ) = 3B(1 − 2µ). (18)
(If the system is anisotropic, additional parameters are
needed to interrelate the moduli, which are directionally
dependent.) This relationship shows that for incompress-
ible materials E = 3G and that the bulk modulus must go
to infinity. Since good elastomers have values of µ close
to 0.5, this upper limit is often a very good approximation
in that an elastomer is three times stiffer in tension than
in shear. However, due to the fact that µ is typically be-
tween 0.3 and 0.4 for glassy or semicrystalline systems, it
follows that Young’s modulus will still always be some-
FIGURE 9 General stress–strain behavior illustrating the phe- what greater than a factor of 2 above the shear modulus.
nomenon of permanent set. This result is a strong indicator that, when a material is