Page 147 - Entrophy Analysis in Thermal Engineering Systems

Entropy and fuel cells 141

where

_ _ T L
W C ¼ Q η ¼ ΔH 1 (9.27)
H C
_ _ _ _ T H (9.28)
Q ¼ W C + Q + Q
in L C
and ΔH is the reaction heat evaluated at T H .
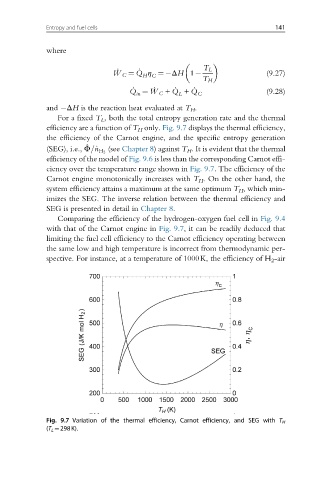
For a fixed T L , both the total entropy generation rate and the thermal
efficiency are a function of T H only. Fig. 9.7 displays the thermal efficiency,
the efficiency of the Carnot engine, and the specific entropy generation
_
(SEG), i.e., Φ=_n H 2 (see Chapter 8) against T H . It is evident that the thermal
efficiency of the model of Fig. 9.6 is less than the corresponding Carnot effi-
ciency over the temperature range shown in Fig. 9.7. The efficiency of the
Carnot engine monotonically increases with T H . On the other hand, the
system efficiency attains a maximum at the same optimum T H , which min-
imizes the SEG. The inverse relation between the thermal efficiency and
SEG is presented in detail in Chapter 8.
Comparing the efficiency of the hydrogen-oxygen fuel cell in Fig. 9.4
with that of the Carnot engine in Fig. 9.7, it can be readily deduced that
limiting the fuel cell efficiency to the Carnot efficiency operating between
the same low and high temperature is incorrect from thermodynamic per-
spective. For instance, at a temperature of 1000K, the efficiency of H 2 -air

Fig. 9.7 Variation of the thermal efficiency, Carnot efficiency, and SEG with T H
(T L ¼298K).