Page 282 - Finite Element Modeling and Simulations with ANSYS Workbench

Structural Vibration and Dynamics 267

= +
2 2
Design
spectrum
Damping ratio 2

Stiffness-proportional

1
dampling: = , = 0
2
Mass-proportional
dampling: = , = 0
2

0
0 1 2 Frequency

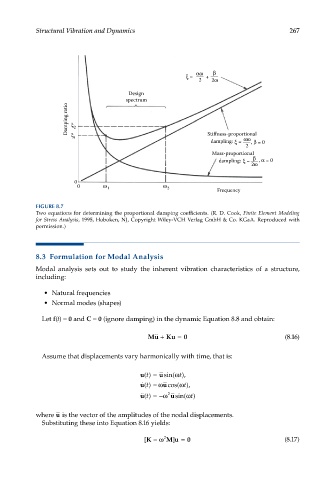
FIGURE 8.7
Two equations for determining the proportional damping coefficients. (R. D. Cook, Finite Element Modeling
for Stress Analysis, 1995, Hoboken, NJ, Copyright Wiley-VCH Verlag GmbH & Co. KGaA. Reproduced with
permission.)

8.3 Formulation for Modal Analysis

Modal analysis sets out to study the inherent vibration characteristics of a structure,
including:

• Natural frequencies
• Normal modes (shapes)

Let f(t) = 0 and C = 0 (ignore damping) in the dynamic Equation 8.8 and obtain:

Mu + Ku = 0 (8.16)

Assume that displacements vary harmonically with time, that is:

ω
u() = usin( t ),
t
ω
u() =ω ucos( t ),

t
t 2 usin( t )
u() =−ω
ω

where u is the vector of the amplitudes of the nodal displacements.
Substituting these into Equation 8.16 yields:
[K −ω 2 M ]u = 0 (8.17)