Page 389 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: NONLINEAR AND CHAOTIC DYNAMICS 365

6 6
4
4
2
.- - 2 .- 0
A
5
- -
x
0
3 0 3 -2
4
-2
4
4 -8
-0.15 -0.10 -0.05 0.00 0.05 0.10 0.15 -0.15 -0.10 -0.05 0.00 0.05 0.10 0.15
(C) Displacement (d) Displacement
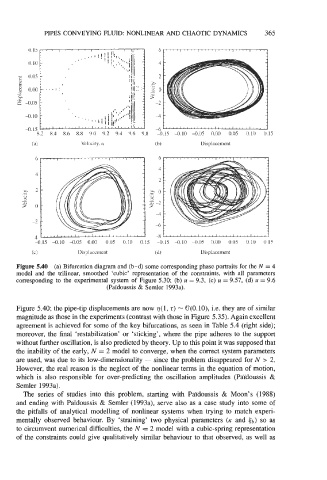
Figure 5.40 (a) Bifurcation diagram and (b-d) some corresponding phase portraits for the N = 4
model and the trilinear, smoothed 'cubic' representation of the constraints, with all parameters
corresponding to the experimental system of Figure 5.30; (b) u = 9.3, (c) u = 9.57, (d) u = 9.6
(Pafdoussis & Semler 1993a).

Figure 5.40; the pipe-tip displacements are now q(1, t) - 0(0.10), i.e. they are of similar
magnitude as those in the experiments (contrast with those in Figure 5.35). Again excellent
agreement is achieved for some of the key bifurcations, as seen in Table 5.4 (right side);
moreover, the final 'restabilization' or 'sticking', where the pipe adheres to the support
without further oscillation, is also predicted by theory. Up to this point it was supposed that
the inability of the early, N = 2 model to converge, when the correct system parameters
are used, was due to its low-dimensionality - since the problem disappeared for N > 2.
However, the real reason is the neglect of the nonlinear terms in the equation of motion,
which is also responsible for over-predicting the oscillation amplitudes (Paidoussis &
Semler 1993a).
The series of studies into this problem, starting with PaYdoussis & Moon's (1988)
and ending with Paidoussis & Semler (1993a), serve also as a case study into some of
the pitfalls of analytical modelling of nonlinear systems when trying to match experi-
mentally observed behaviour. By 'straining' two physical parameters (K and (b) so as
to circumvent numerical difficulties, the N = 2 model with a cubic-spring representation
of the constraints could give qualitatively similar behaviour to that observed, as well as