Page 395 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

PIPES CONVEYING FLUID: NONLINEAR AND CHAOTIC DYNAMICS 371

pipe in the course of oscillation and (ii) to ensure that it is not overtightened onto thc
pipe, thus deforming its free end.
Several elastomer pipes were used (typically, Di = 6.3 mm, Do = 15.7mm, L =
470mm), giving fi = 0.125-0.150 and y 2: 20, and eight different end-masses, made
of plastic or metal, JM. = 2.4-37.8 g; this corresponds to values of the dimensionless
added mass,

(5.139)

ranging from p = 0.023 to 0.380.
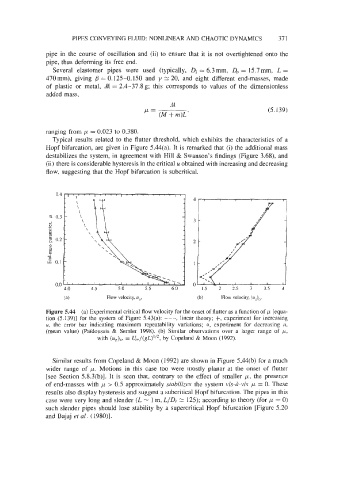
Typical results related to the flutter threshold, which exhibits the characteristics of a
Hopf bifurcation, are given in Figure 5.44(a). It is remarked that (i) the additional mass
destabilizes the system, in agreement with Hill & Swanson's findings (Figure 3.68), and
(ii) there is considerable hysteresis in the critical u obtained with increasing and decreasing
flow, suggesting that the Hopf bifurcation is subcritical.

0.4
4 , I t

0.3
3-

0.0 I
1.5 2 2.5 3 3.5 4
(a) Flow velocity, if,, (b) Flow velocity, (u&~
Figure 5.44 (a) Experimental critical flow velocity for the onset of flutter as a function of p [equa-
tion (5.1391 for the system of Figure 5.43(a): ---, linear theory; +, experiment for increasing
u, the error bar indicating maximum repeatability variations; 0, experiment for decreasing u,
(mean value) (PaYdoussis & Semler 1998). (b) Similar observations over a larger range of p,
with (u~)~~ V,,/(gL)'/*, by Copeland & Moon (1992).
=

Similar results from Copeland & Moon (1992) are shown in Figure 5-44(b) for a much
wider range of p. Motions in this case too were mostly planar at the onset of flutter
[see Section 5.8.3(b)]. It is seen that, contrary to the effect of smaller p, the presence
of end-masses with p > 0.5 approximately stabilizes the system vis-&vis /* = 0. These
results also display hysteresis and suggest a subcritical Hopf bifurcation. The pipes in this
case were very long and slender (L - 1 m, LIDi 2: 125); according to theory (for p = 0)
such slender pipes should lose stability by a supercritical Hopf bifurcation [Figure 5.20
and Bajaj et al. (1980)l.