Page 398 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

374 SLENDER STRUCTURES AND AXIAL FLOW

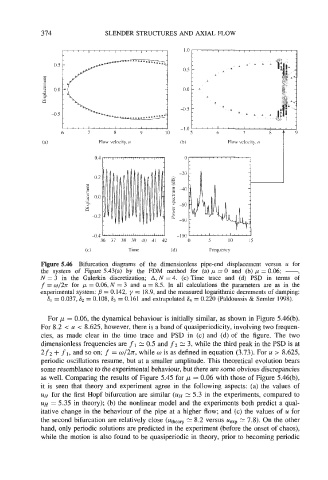
Figure 5.46 Bifurcation diagrams of the dimensionless pipe-end displacement versus u for
the system of Figure 5.43(a) by the FDM method for (a) p = 0 and (b) p = 0.06; -,
N = 3 in the Galerkin discretization; A, N = 4. (c) Time trace and (d) PSD in terms of
f = w/2n for p = 0.06, N = 3 and u = 8.5. In all calculations the parameters are as in the
experimental system: B = 0.142, y = 18.9, and the measured logarithmic decrements of damping:
6, = 0.037, SZ = 0.108,63 = 0.161 and extrapolated 64 = 0.220 (Pdidoussis & Semler 1998).

For p = 0.06, the dynamical behaviour is initially similar, as shown in Figure 5.46(b).
For 8.2 < u < 8.625, however, there is a band of quasiperiodicity, involving two frequen-
cies, as made clear in the time trace and PSD in (c) and (d) of the figure. The two
dimensionless frequencies are fl 1: 0.5 and f2 1: 3, while the third peak in the PSD is at
2f2 + fl, and so on; f = w/2n, while w is as defined in equation (3.73). For u > 8.625,
periodic oscillations resume, but at a smaller amplitude. This theoretical evolution bears
some resemblance to the experimental behaviour, but there are some obvious discrepancies
as well. Comparing the results of Figure 5.45 for p = 0.06 with those of Figure 5.46(b),
it is seen that theory and experiment agree in the following aspects: (a) the values of
UH for the first Hopf bifurcation are similar (u~ 5.3 in the experiments, compared to
1:
UH = 5.35 in theory); (b) the nonlinear model and the experiments both predict a qual-
itative change in the behaviour of the pipe at a higher flow; and (c) the values of u for
the second bifurcation are relatively close (uheory 1: 8.2 versus uexp 1: 7.8). On the other
hand, only periodic solutions are predicted in the experiment (before the onset of chaos),
while the motion is also found to be quasiperiodic in theory, prior to becoming periodic