Page 401 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)
P. 401
PIPES CONVEYING FLUID: NONLINEAR AND CHAOTIC DYNAMICS 377
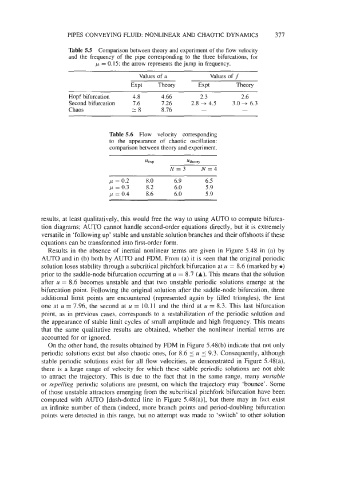
Table 5.5 Comparison between theory and experiment of the flow velocity
and the frequency of the pipe corresponding to the three bifurcations, for
p = 0.15; the arrow represents the jump in frequency.
Values of u Values of f
Expt Theory Expt Theory
Hopf bifurcation 4.8 4.66 2.3 2.6
Second bifurcation 7.6 7.26 2.8 + 4.5 3.0 + 6.3
Chaos -8 8.76 - -
Table 5.6 Flow velocity corresponding
to the appearance of chaotic oscillation:
comparison between theory and experiment.
Uexp Utheory
N=3 N=4
p = 0.2 8.0 6.9 6.5
p = 0.3 8.2 6.0 5.9
p = 0.4 8.6 6.0 5.9
results, at least qualitatively, this would free the way to using AUTO to compute bifurca-
tion diagrams; AUTO cannot handle second-order equations directly, but it is extremely
versatile in ‘following up’ stable and unstable solution branches and their offshoots if these
equations can be transformed into first-order form.
Results in the absence of inertial nonlinear terms are given in Figure 5.48 in (a) by
AUTO and in (b) both by AUTO and FDM. From (a) it is seen that the original periodic
solution loses stability through a subcritical pitchfork bifurcation at u = 8.6 (marked by 0)
prior to the saddle-node bifurcation occurring at u = 8.7 (A). This means that the solution
after u = 8.6 becomes unstable and that two unstable periodic solutions emerge at the
bifurcation point. Following the original solution after the saddle-node bifurcation, three
additional limit points are encountered (represented again by filled triangles), the first
one at u = 7.96, the second at u = 10.11 and the third at u = 8.3. This last bifurcation
point, as in previous cases, corresponds to a restabilization of the periodic solution and
the appearance of stable limit cycles of small amplitude and high frequency. This means
that the same qualitative results are obtained, whether the nonlinear inertial terms are
accounted for or ignored.
On the other hand, the results obtained by FDM in Figure 5.48(b) indicate that not only
periodic solutions exist but also chaotic ones, for 8.6 5 u 5 9.3. Consequently, although
stable periodic solutions exist for all flow velocities, as demonstrated in Figure 5.48(a),
there is a large range of velocity for which these stable periodic solutions are not able
to attract the trajectory. This is due to the fact that in the same range, many unstable
or repelling periodic solutions are present, on which the trajectory may ‘bounce’. Some
of those unstable attractors emerging from the subcritical pitchfork bifurcation have been
computed with AUTO [dash-dotted line in Figure 5.48(a)], but there may in fact exist
an infinite number of them (indeed, more branch points and period-doubling bifurcation
points were detected in this range, but no attempt was made to ‘switch’ to other solution