Page 404 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

SLENDER STRUCTURES AND AXIAL FLOW

Ir v r i p -
3.81 *’
3.95 4.1 4.25 4.4
I
3.65 3.80 3.95
2.60 .’
a I 3.25 3.40
d 3.10 3.25 3.40
$ 1.89 .’ - I \ I
-
2 2.80 I 2.95 3.10
2.50 2.65
0.746 *. c
2.20
1.90 2.05 2.20 2.35
Of I t 1

Top view
of path

(4
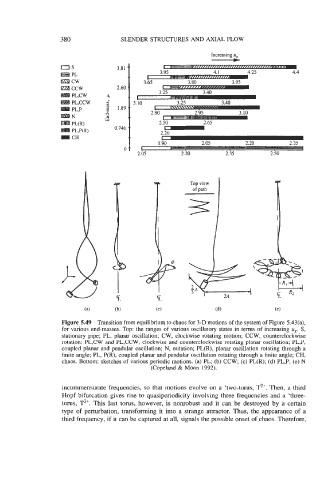
Figure 5.49 Transition from equilibrium to chaos for 3-D motions of the system of Figure 5.43(a),
for various end-masses. Top: the ranges of various oscillatory states in terms of increasing ug. S,
stationary pipe; PL, planar oscillation; CW, clockwise rotating motion; CCW, counterclockwise
rotation: PL,CW and PL,CCW, clockwise and counterclockwise rotating planar oscillation; PL,P,
coupled planar and pendular oscillation; N, nutation; PL(R), planar oscillation rotating through a
finite angle; PL, P(R), coupled planar and pendular oscillation rotating through a finite angle; CH,
chaos. Bottom: sketches of various periodic motions. (a) PL; (b) CCW; (c) PL(R); (d) PL,P; (e) N
(Copeland & Moon 1992).

incommensurate frequencies, so that motions evolve on a ‘two-torus, T2’. Then, a third
Hopf bifurcation gives rise to quasiperiodicity involving three frequencies and a ‘three-
torus, T3’. This last torus, however, is nonrobust and it can be destroyed by a certain
type of perturbation, transforming it into a strange attractor. Thus, the appearance of a
third frequency, if it can be captured at all, signals the possible onset of chaos. Therefore,