Page 396 - Fluid-Structure Interactions Slender Structure and Axial Flow (Volume 1)

372 SLENDER STRUCTURES AND AXIAL FLOW

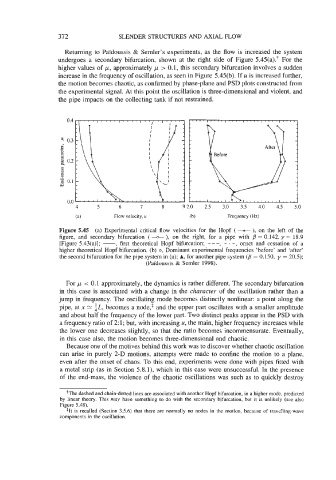
Returning to Paydoussis & Semler’s experiments, as the flow is increased the system
undergoes a secondary bifurcation, shown at the right side of Figure 5.45(a).+ For the
higher values of p, approximately p > 0.1, this secondary bifurcation involves a sudden
increase in the frequency of oscillation, as seen in Figure 5.45(b). If u is increased further,
the motion becomes chaotic, as confirmed by phase-plane and PSD plots constructed from
the experimental signal. At this point the oscillation is three-dimensional and violent, and
the pipe impacts on the collecting tank if not restrained.

4 5 6 I 8 9 2.0 2.5 3.0 3.5 4.0 4.5 5.0
(a) Flow velocity, u (b) Frequency (Hz)
Figure 5.45 (a) Experimental critical flow velocities for the Hopf ( -*- ), on the left of the
figure, and secondary bifurcation ( - on the right, for a pipe with = 0.142, y = 18.9
),
,
[Figure 5.43(a)]; - first theoretical Hopf bifurcation; - - -, - . -, onset and cessation of a
higher theoretical Hopf bifurcation. (b) 0, Dominant experimental frequencies ‘before’ and ‘after’
the second bifurcation for the pipe system in (a); A, for another pipe system (B = 0.150, y = 20.5);
(PaTdoussis & Semler 1998).

For p < 0.1 approximately, the dynamics is rather different. The secondary bifurcation
in this case is associated with a change in the character of the oscillation rather than a
jump in frequency. The oscillating mode becomes distinctly nonlinear: a point along the
pipe, at x 2: iL, becomes a node,$ and the upper part oscillates with a smaller amplitude
and about half the frequency of the lower part. Two distinct peaks appear in the PSD with
a frequency ratio of 2: 1; but, with increasing u, the main, higher frequency increases while
the lower one decreases slightly, so that the ratio becomes incommensurate. Eventually,
in this case also, the motion becomes three-dimensional and chaotic.
Because one of the motives behind this work was to discover whether chaotic oscillation
can arise in purely 2-D motions, attempts were made to confine the motion to a plane,
even after the onset of chaos. To this end, experiments were done with pipes fitted with
a metal strip (as in Section 5.8.1), which in this case were unsuccessful. In the presence
of the end-mass, the violence of the chaotic oscillations was such as to quickly destroy

+The dashed and chain-dotted lines are associated with another Hopf bifurcation, in a higher mode, predicted
by linear theory. This may have something to do with the secondary bifurcation, but it is unlikely (see also
Figure 5.48).
*It is recalled (Section 3.5.6) that there are normally no nodes in the motion, because of travelling-wave
components in the oscillation.