Page 171 - T. Anderson-Fracture Mechanics - Fundamentals and Applns.-CRC (2005)

1656_C003.fm Page 151 Monday, May 23, 2005 5:42 PM

Elastic-Plastic Fracture Mechanics 151

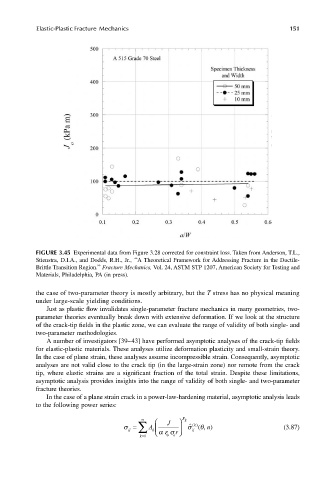
FIGURE 3.45 Experimental data from Figure 3.28 corrected for constraint loss. Taken from Anderson, T.L.,
Stienstra, D.I.A., and Dodds, R.H., Jr., ‘‘A Theoretical Framework for Addressing Fracture in the Ductile-
Brittle Transition Region.’’ Fracture Mechanics, Vol. 24, ASTM STP 1207, American Society for Testing and
Materials, Philadelphia, PA (in press).

the case of two-parameter theory is mostly arbitrary, but the T stress has no physical meaning
under large-scale yielding conditions.
Just as plastic flow invalidates single-parameter fracture mechanics in many geometries, two-
parameter theories eventually break down with extensive deformation. If we look at the structure
of the crack-tip fields in the plastic zone, we can evaluate the range of validity of both single- and
two-parameter methodologies.
A number of investigators [39–43] have performed asymptotic analyses of the crack-tip fields
for elastic-plastic materials. These analyses utilize deformation plasticity and small-strain theory.
In the case of plane strain, these analyses assume incompressible strain. Consequently, asymptotic
analyses are not valid close to the crack tip (in the large-strain zone) nor remote from the crack
tip, where elastic strains are a significant fraction of the total strain. Despite these limitations,
asymptotic analysis provides insights into the range of validity of both single- and two-parameter
fracture theories.
In the case of a plane strain crack in a power-law-hardening material, asymptotic analysis leads
to the following power series:
s k
∞


J
ij ∑
σ = A k αεσ r   σ ij k () (, n) (3.87)
θ ˆ
k=1  o o