Page 134 - Fundamentals of Communications Systems

4.10 Chapter Four

0

−10

−20

−30
)
G y z (f
−40

−50

−60

−70
−5000 −4000 −3000 −2000 −1000 0 1000 2000 3000 4000 5000
Frequency, f, Hz
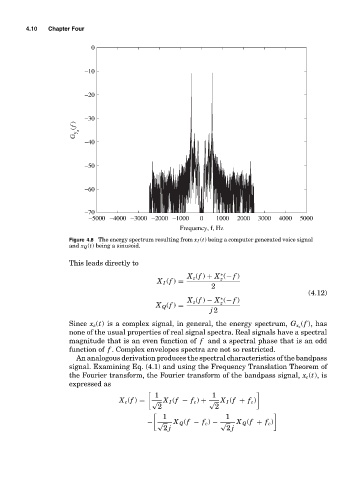
Figure 4.8 The energy spectrum resulting from x I (t) being a computer generated voice signal
and x Q (t) being a sinusoid.

This leads directly to

X z (f ) + X (− f )
∗
z
X I (f ) =
2
(4.12)
X z (f ) − X (− f )
∗
z
X Q (f ) =
j 2
(f ), has
Since x z (t) is a complex signal, in general, the energy spectrum, G x z
none of the usual properties of real signal spectra. Real signals have a spectral
magnitude that is an even function of f and a spectral phase that is an odd
function of f . Complex envelopes spectra are not so restricted.
An analogous derivation produces the spectral characteristics of the bandpass
signal. Examining Eq. (4.1) and using the Frequency Translation Theorem of
the Fourier transform, the Fourier transform of the bandpass signal, x c (t), is
expressed as
1 1

X c (f ) = √ X I (f − f c ) + √ X I (f + f c )
2 2

1 1
− √ X Q (f − f c ) − √ X Q (f + f c )
2 j 2 j