Page 149 - Fundamentals of Probability and Statistics for Engineers

132 Fundamentals of Probability and Statistics for Engineers

For all y, Equation (5.25) yields

2
1
X dg y†
j

1
f y†ˆ f ‰g y†Š
Y

j
jˆ1 dy

1 1 1 1 5:26†
ˆ ‡
2 1 ‡ y 2 2 1 ‡ y 2
1
ˆ ;
1 < y < 1;
2
1 ‡ y †
a result identical to the solution for Example 5.4 [see Equation (5.18)].
2
Example 5.7. Problem: determine the pdf of Y ˆ X where X is normally

distributed according to
1
x =2
2
f x†ˆ e ;
1 < x < 1: 5:27†
X 1=2
2 †
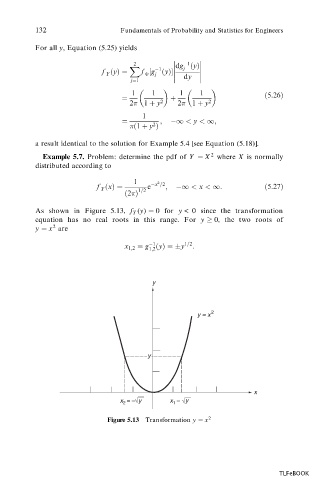
As shown in Figure 5.13, f Y (y) ˆ 0 for y < 0 since the transformation
equation has no real roots in this range. For y 0, the two roots of
2
y ˆ x are

1
x 1;2 ˆ g y†ˆ y 1=2 :
1;2
y

2
y = x

y

x
x = –√y x = √y
1
2
Figure 5.13 Transformation y ˆ x 2

TLFeBOOK