Page 157 - Fundamentals of Water Treatment Unit Processes : Physical, Chemical, and Biological

112 Fundamentals of Water Treatment Unit Processes: Physical, Chemical, and Biological

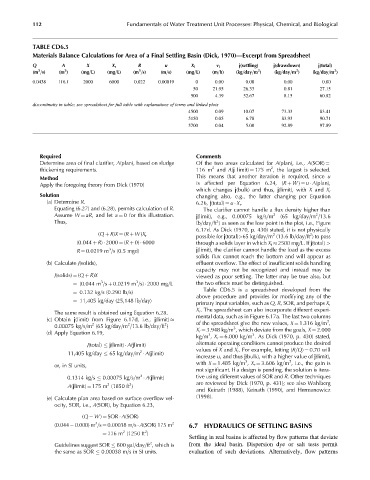
TABLE CD6.5
Materials Balance Calculations for Area of a Final Settling Basin (Dick, 1970)—Excerpt from Spreadsheet
Q A X X r R u X i v i j(settling) j(drawdown) j(total)
3
2
2
2
2
3
(m =s) (m ) (mg=L) (mg=L) (m =s) (m=s) (mg=L) (m=h) (kg=day=m ) (kg=day=m ) (kg=day=m )
0.0438 116.1 2000 6000 0.022 0.00019 0 0.00 0.00 0.00 0.00
50 21.95 26.33 0.81 27.15
500 4.39 52.67 8.15 60.82
discontinuity in table; see spreadsheet for full table with explanations of terms and linked plots
4500 0.09 10.07 73.33 83.41
5150 0.05 6.78 83.93 90.71
5700 0.04 5.00 92.89 97.89

Required Comments
Determine area of final clarifier, A(plan), based on sludge Of the two areas calculated for A(plan), i.e., A(SOR) ¼
2
2
thickening requirements. 116 m and A(j limit) ¼ 175 m , the largest is selected.
Method This means that another iteration is required, since u
Apply the foregoing theory from Dick (1970) is affected per Equation 6.24, (R þ W ) ¼ u A(plan),
which changes j(bulk) and thus, j(limit), with X and X r
Solution changing also, e.g., the latter changing per Equation
(a) Determine R. 6.26, j(total) ¼ u X r .
Equating (6.27) and (6.28), permits calculation of R. The clarifier cannot handle a flux density higher than
2
Assume W ¼ aR, and let a ¼ 0 for this illustration. j(limit), e.g., 0.00075 kg=s=m 2 (65 kg=day=m =13.6
2
Thus, lb=day=ft ) as seen as the low point in the plot, i.e., Figure
6.17d. As Dick (1970, p. 430) stated, it is not physically
(Q þ R)X ¼ (R þ W )X r 2 2
possible for j(total)>65 kg=day=m (13.6 lb=day=ft ) to pass
(0.044 þ R) 2000 ¼ (R þ 0) 6000 through a solids layer in which X i 2500 mg=L. If j(total) >
3
R ¼ 0.0219 m =s (0.5 mgd) j(limit), the clarifier cannot handle the load as the excess
solids flux cannot reach the bottom and will appear as
(b) Calculate J(solids), effluent overflow. The effect of insufficient solids handling
capacity may not be recognized and instead may be
J(solids) ¼ (Q þ R)X viewed as poor settling. The latter may be true also, but
3
3
¼ (0.044 m =s þ 0.0219 m =s) 2000 mg=L the two effects must be distinguished.
Table CD6.5 is a spreadsheet developed from the
¼ 0.132 kg=s (0.290 lb=s)
above procedure and provides for modifying any of the
¼ 11,405 kg=day (25,148 lb=day)
primary input variables, such as Q, R, SOR, and perhaps X,
X r . The spreadsheet can also incorporate different experi-
The same result is obtained using Equation 6.28.
mental data, such as in Figure 6.17a. The last two columns
3
(c) Obtain j(limit) from Figure 6.17d, i.e., j(limit) of the spreadsheet give the new values, X ¼ 1.316 kg=m ,
2
2
2
0.00075 kg=s=m (65 kg=day=m =13.6 lb=day=ft ) 3
(d) Apply Equation 6.19, X r ¼ 3.948 kg=m , which deviate from the goals, X ¼ 2.000
3
3
kg=m , X r ¼ 6.000 kg=m . As Dick (1970, p. 430) stated,
J(total) j(limit) A(jlimit) alternate operating conditions cannot produce the desired
values of X and X r . For example, letting (R=Q) ¼ 0.70 will
2
11,405 kg=day 65 kg=day=m A(jlimit)
increase u, and thus j(bulk), with a higher value of j(limit),
3
3
with X ¼ 1.485 kg=m , X r ¼ 3.606 kg=m , i.e., the gain is
or, in SI units,
not significant. If a design is pending, the solution is itera-
2
0.1314 kg=s 0.00075 kg=s=m A(jlimit) tive using different values of SOR and R. Other techniques
2
2
A(jlimit) ¼ 175 m (1850 ft ) are reviewed by Dick (1970, p. 431); see also Wahlberg
and Keinath (1988), Keinath (1990), and Hermanowicz
(e) Calculate plan area based on surface overflow vel- (1998).
ocity, SOR, i.e., A(SOR), by Equation 6.23,
(Q W ) ¼ SOR A(SOR)
3
(0.044 0.000) m =s ¼ 0.00038 m=s A(SOR) 175 m 2 6.7 HYDRAULICS OF SETTLING BASINS
2
2
¼ 116 m (1250 ft )
Settling in real basins is affected by flow patterns that deviate
2
Guidelines suggest SOR 800 gal=day=ft , which is from the ideal basin. Dispersion dye or salt tests permit
the same as SOR 0.00038 m=s in SI units. evaluation of such deviations. Alternatively, flow patterns