Page 190 - Fundamentals of Water Treatment Unit Processes : Physical, Chemical, and Biological

Grit Chambers 145

Transition Converging section Throat Diverging section

h L
0.75 m (2.40 ft) H 0.67 m (2.19 ft) 0.44 m (1.44 ft)

a
H b
ΔZ=0.08 m (0.21 ft)

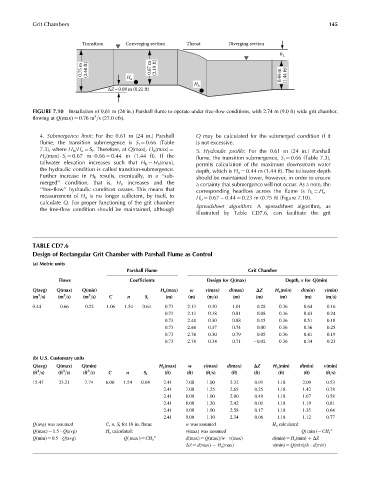
FIGURE 7.10 Installation of 0.61 m (24 in.) Parshall flume to operate under free-flow conditions, with 2.74 m (9.0 ft) wide grit chamber,
3
flowing at Q(max) ¼ 0.76 m =s (27.0 cfs).
4. Submergence limit: For the 0.61 m (24 in.) Parshall Q may be calculated for the submerged condition if it
flume, the transition submergence is S t ¼ 0.66 (Table is not excessive.
7.3), where H b =H a ¼ S t . Therefore, at Q(max), H b (max) ¼ 5. Hydraulic profile: For the 0.61 m (24 in.) Parshall
H a (max) S t ¼ 0.67 m 0.66 ¼ 0.44 m (1.44 ft). If the flume, the transition submergence, S t ¼ 0.66 (Table 7.3),
tailwater elevation increases such that H b ¼ H b (max), permits calculation of the maximum downstream water
the hydraulic condition is called transition-submergence. depth, which is H a ¼ 0.44 m (1.44 ft). The tailwater depth
Further increase in H b results, eventually, in a ‘‘sub- should be maintained lower, however, in order to ensure
merged’’ condition, that is, H a increases and the a certainty that submergence will not occur. As a note, the
‘‘free-flow’’ hydraulic condition ceases. This means that
corresponding headloss across the flume is h L ¼ H a
measurement of H a is no longer sufficient, by itself, to H b ¼ 0.67 0.44 ¼ 0.23 m (0.75 ft) (Figure 7.10).
calculate Q. For proper functioning of the grit chamber
the free-flow condition should be maintained, although Spreadsheet algorithm: A spreadsheet algorithm, as
illustrated by Table CD7.6, can facilitate the grit

TABLE CD7.6
Design of Rectangular Grit Chamber with Parshall Flume as Control
(a) Metric units
Parshall Flume Grit Chamber
Flows Coefficients Design for Q(max) Depth, v for Q(min)
Q(avg) Q(max) Q(min) H a (max) w v(max) d(max) DZ H a (min) d(min) v(min)
3
3
3
(m =s) (m =s) (m =s) C n S t (m) (m) (m=s) (m) (m) (m) (m) (m=s)
0.44 0.66 0.22 1.06 1.54 0.64 0.73 2.13 0.30 1.01 0.28 0.36 0.64 0.16
0.73 2.13 0.38 0.81 0.08 0.36 0.43 0.24
0.73 2.44 0.30 0.88 0.15 0.36 0.51 0.18
0.73 2.44 0.37 0.74 0.00 0.36 0.36 0.25
0.73 2.74 0.30 0.79 0.05 0.36 0.41 0.19
0.73 2.74 0.34 0.71 0.02 0.36 0.34 0.23

(b) U.S. Customary units
Q(avg) Q(max) Q(min) H a (max) w v(max) d(max) DZ H a (min) d(min) v(min)
3
3
3
(ft =s) (ft =s) (ft =s) C n S t (ft) (ft) (ft=s) (ft) (ft) (ft) (ft) (ft=s)
15.47 23.21 7.74 6.00 1.54 0.64 2.41 7.00 1.00 3.32 0.91 1.18 2.09 0.53
2.41 7.00 1.25 2.65 0.25 1.18 1.42 0.78
2.41 8.00 1.00 2.90 0.49 1.18 1.67 0.58
2.41 8.00 1.20 2.42 0.01 1.18 1.19 0.81
2.41 9.00 1.00 2.58 0.17 1.18 1.35 0.64
2.41 9.00 1.10 2.34 0.06 1.18 1.12 0.77
Q(avg) was assumed C, n, S t for 18 in. flume w was assumed H a calculated:
Q(max) ¼ 1.5 Q(avg) H a calculated: v(max) was assumed Q( min )¼CH a n
Q(min) ¼ 0.5 Q(avg) Q( max )¼CH a n d(max) ¼ Q(max)=w v(max) d(min) ¼ H a (min) þ DZ
DZ ¼ d(max) H a (max) v(min) ¼ Q(min)=b d(min)