Page 219 - Fundamentals of Water Treatment Unit Processes : Physical, Chemical, and Biological

174 Fundamentals of Water Treatment Unit Processes: Physical, Chemical, and Biological

15 C r is the mass concentration of the air bubbles that
Conditions
T =20°C must be generated to satisfy the demand by the
d =40 μm particle number concentration in order to float the
b
ρ =1010 kg/m 3 particles; also termed, the air ‘‘released’’ by gas
P
3
precipitation (kg gas=m water)
10
2. Bubble number concentration N b ,
v pb (m/h) B=10 bubble/particle F b
3
pd =6 (8:15)
N b ¼
b
5
in which
is the bubble number concentration (#
N b
B=2 bubble/particle 3
bubbles=m water)
B =1 bubble/particle d b is the mean diameter of air bubbles (cm)
0
0 50 100 150 200 250 300
After substituting (8.14) in (8.15),
d p (μm)
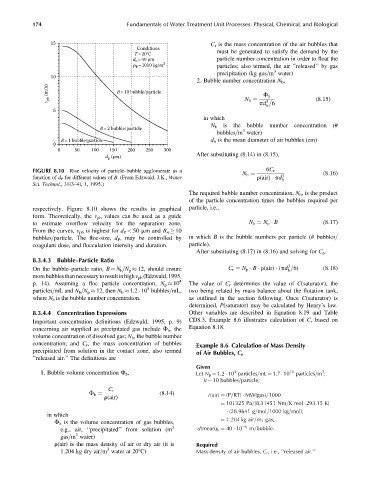
FIGURE 8.10 Rise velocity of particle–bubble agglomerate as a 6C r (8:16)
function of d P for different values of B. (From Edzwald, J.K., Water N b ¼ r(air) pd 3
b
Sci. Technol., 31(3–4), 1, 1995.)
The required bubble number concentration, N b , is the product
of the particle concentration times the bubbles required per
respectively. Figure 8.10 shows the results in graphical particle, i.e.,
form. Theoretically, the v pb values can be used as a guide
to estimate overflow velocity for the separation zone. N b ¼ N p B (8:17)
From the curves, v pb is highest for d P < 50 mm and B n 10
bubbles=particle. The floc-size, d P , may be controlled by in which B is the bubble numbers per particle (# bubbles=
coagulant dose, and flocculation intensity and duration. particle).
After substituting (8.17) in (8.16) and solving for C r ,
8.3.4.3 Bubble–Particle Ratio
3
=
On the bubble–particle ratio, B ¼ N b =N p 12, should ensure C r ¼ N p B r(air) (pd 6) (8:18)
b
morebubblesthannecessarytoresultinhighv pb (Edzwald,1995,
p. 14). Assuming a floc particle concentration, N p 10 4 The value of C r determines the value of C(saturator), the
5
particles=mL and N b =N p 12, then N b 1.2 10 bubbles=mL, two being related by mass balance about the flotation tank,
where N b is the bubble number concentration. as outlined in the section following. Once C(saturator) is
determined, P(saturator) may be calculated by Henry’s law.
8.3.4.4 Concentration Expressions Other variables are described in Equation 8.19 and Table
Important concentration definitions (Edzwald, 1995, p. 9) CD8.3. Example 8.6 illustrates calculation of C r based on
concerning air supplied as precipitated gas include F b , the Equation 8.18.
volume concentration of dissolved gas; N b , the bubble number
concentration; and C r , the mass concentration of bubbles Example 8.6 Calculation of Mass Density
precipitated from solution in the contact zone, also termed
of Air Bubbles, C r
‘‘released air.’’ The definitions are
Given
1. Bubble volume concentration F b , Let N p ¼ 1.2 10 particles=mL ¼ 1.7 10 10 particles=m ;
3
4
B ¼ 10 bubbles=particle;
C r
(8:14)
F b ¼ r(air) ¼ (P=RT) MW(gas)=1000
r(air)
¼ 101325 Pa=(8:31451 Nm=K mol 293:15 K)
(28:9641 g=mol=1000 kg=mol);
in which
¼ 1:204 kg air=m 3 gas;
F b is the volume concentration of gas bubbles, 6
e.g., air, ‘‘precipitated’’ from solution (m 3 d(mean) b ¼ 40 10 m=bubble:
3
gas=m water)
r(air) is the mass density of air or dry air (it is Required
3
1.204 kg dry air=m water at 208C) Mass density of air bubbles, C r , i.e., ‘‘released air.’’