Page 873 - Fundamentals of Water Treatment Unit Processes : Physical, Chemical, and Biological

828 Appendix E: Porous Media Hydraulics

0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34
40
38
HGL
36
t=0 h
34
h (valve E)t=0 h
HGL L
32
t=2 h
h (valve E)t=2 h
L
30 Headwater
HGL
28
t=4 h
h (valve E)t=4 h
L
26
HGL (valve E)t=6 h
h L
24
A t=6 h
22
20
B
18
16 Mono media
C
14
12
D Tail water
10
8
Support
6
gravel
4
E
2 X
Valve is open fully after 6 h
0

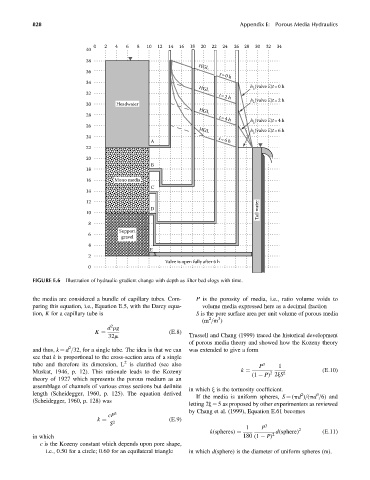
FIGURE E.6 Illustration of hydraulic gradient change with depth as filter bed clogs with time.

the media are considered a bundle of capillary tubes. Com- P is the porosity of media, i.e., ratio volume voids to
paring this equation, i.e., Equation E.5, with the Darcy equa- volume media expressed here as a decimal fraction
tion, K for a capillary tube is S is the pore surface area per unit volume of porous media
2
3
(m =m )
2
d rg
(E:8)
32m Trussell and Chang (1999) traced the historical development
K ¼
of porous media theory and showed how the Kozeny theory
2
and thus, k ¼ d =32, for a single tube. The idea is that we can was extended to give a form
see that k is proportional to the cross-section area of a single
2
tube and therefore its dimension, L is clarified (see also P 3 1
Muskat, 1946, p. 12). This rationale leads to the Kozeny k ¼ (1 P) 2jS 2 (E:10)
2
theory of 1927 which represents the porous medium as an
assemblage of channels of various cross sections but definite
in which j is the tortuosity coefficient.
length (Scheidegger, 1960, p. 125). The equation derived 2 3
If the media is uniform spheres, S ¼ (pd )=(pd =6) and
(Scheidegger, 1960, p. 128) was
letting 2j ¼ 5 as proposed by other experimenters as reviewed
by Chang et al. (1999), Equation E.61 becomes
cP 3
(E:9)
S 3
k ¼ 2
1 P 2
d(sphere) (E:11)
k(spheres) ¼ 2
in which 180 (1 P)
c is the Kozeny constant which depends upon pore shape,
i.e., 0.50 for a circle; 0.60 for an equilateral triangle in which d(sphere) is the diameter of uniform spheres (m).