Page 360 - gas transport in porous media

362
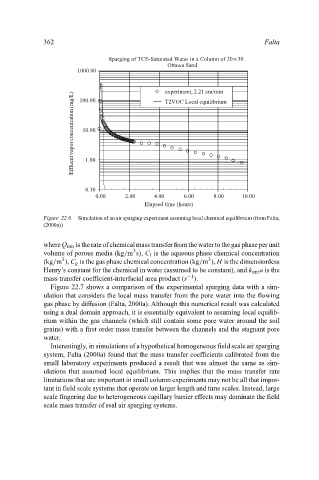
Sparging of TCE-Saturated Water in a Column of 20× 30
Ottawa Sand Falta
1000.00
experiment, 2.21 cm/min
Effluent vapor concentration (mg/L) 10.00
100.00
T2VOC Local equilibrium

1.00

0.10
0.00 2.00 4.00 6.00 8.00 10.00
Elapsed time (hours)

Figure 22.6. Simulation of an air sparging experiment assuming local chemical equilibrium (from Falta,
(2000a))

where Q imt is the rate of chemical mass transfer from the water to the gas phase per unit
3
volume of porous media (kg/m s), C l is the aqueous phase chemical concentration
3 3
(kg/m ), C g is the gas phase chemical concentration (kg/m ), H is the dimensionless
Henry’s constant for the chemical in water (assumed to be constant), and k imt a is the
mass transfer coefficient-interfacial area product (s −1 ).
Figure 22.7 shows a comparison of the experimental sparging data with a sim-
ulation that considers the local mass transfer from the pore water into the flowing
gas phase by diffusion (Falta, 2000a). Although this numerical result was calculated
using a dual domain approach, it is essentially equivalent to assuming local equilib-
rium within the gas channels (which still contain some pore water around the soil
grains) with a first order mass transfer between the channels and the stagnant pore
water.
Interestingly, in simulations of a hypothetical homogeneous field scale air sparging
system, Falta (2000a) found that the mass transfer coefficients calibrated from the
small laboratory experiments produced a result that was almost the same as sim-
ulations that assumed local equilibrium. This implies that the mass transfer rate
limitations that are important in small column experiments may not be all that impor-
tant in field scale systems that operate on larger length and time scales. Instead, large
scale fingering due to heterogeneous capillary barrier effects may dominate the field
scale mass transfer of real air sparging systems.