Page 211 - Geochemical Anomaly and Mineral Prospectivity Mapping in GIS

Knowledge-Driven Modeling of Mineral Prospectivity 213

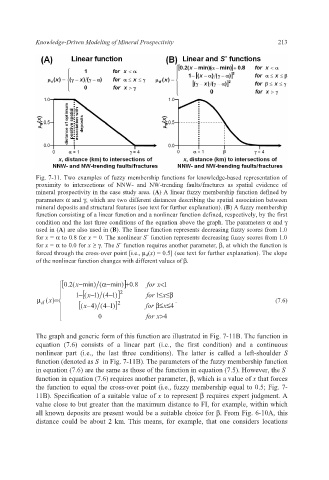
Fig. 7-11. Two examples of fuzzy membership functions for knowledge-based representation of
proximity to intersections of NNW- and NW-trending faults/fractures as spatial evidence of
mineral prospectivity in the case study area. (A) A linear fuzzy membership function defined by
parameters α and γ, which are two different distances describing the spatial association between
mineral deposits and structural features (see text for further explanation). (B) A fuzzy membership
function consisting of a linear function and a nonlinear function defined, respectively, by the first
condition and the last three conditions of the equation above the graph. The parameters α and γ
used in (A) are also used in (B). The linear function represents decreasing fuzzy scores from 1.0
–
for x = α to 0.8 for x = 0. The nonlinear S function represents decreasing fuzzy scores from 1.0
–
for x = α to 0.0 for x ≥ γ. The S function requires another parameter, β, at which the function is
forced through the cross-over point [i.e., μ d (x) = 0.5] (see text for further explanation). The slope
of the nonlinear function changes with different values of β.

[ ­ .0 ( 2 x −min) α ( −min) ]+ 8.0 for x <1
° − 1 [ − )1(x 4 ( − ] ) 1 2 for ≤ 1 ≤ x β
μ (x = ) ° 2 . (7.6)
®
d
° [ − )4(x 4 ( − ] ) 1 for β ≤x ≤4
° 0 for x >4
¯

The graph and generic form of this function are illustrated in Fig. 7-11B. The function in
equation (7.6) consists of a linear part (i.e., the first condition) and a continuous
nonlinear part (i.e., the last three conditions). The latter is called a left-shoulder S
–
function (denoted as S in Fig. 7-11B). The parameters of the fuzzy membership function
–
in equation (7.6) are the same as those of the function in equation (7.5). However, the S
function in equation (7.6) requires another parameter, β, which is a value of x that forces
the function to equal the cross-over point (i.e., fuzzy membership equal to 0.5; Fig. 7-
11B). Specification of a suitable value of x to represent β requires expert judgment. A
value close to but greater than the maximum distance to FI, for example, within which
all known deposits are present would be a suitable choice for β. From Fig. 6-10A, this
distance could be about 2 km. This means, for example, that one considers locations