Page 139 - Geothermal Energy Renewable Energy and The Environment

Resource Assessments 125

The sIGnIFIcance oF heaT capacITy
Once temperature and volume for a reservoir have been established, the volumetric heat content can
be computed from Equation 7.1. The only variable left to establish is the heat capacity.
As previously discussed in Chapter 3, the heat capacity is a function of the mineral, or minerals,
present and the temperature. The heat capacity temperature dependence for a mineral is usually
expressed as a power function of the temperature, such as,

−2
−3
C = k − k × T −0.5 + k × T + k × T , (7.2)
p
3
0
1
2
(Berman 1988; Berman and Brown 1985) where k is a fitting coefficient derived from analysis of
i
experimental measurements of heat capacities of individual minerals. Other versions of this rela-
tionship have been proposed (e.g., Helgeson et al. 1978; see review by Navarotsky 1995) and used
to generate heat capacity values for individual minerals. In most instances, the differences between
different fitting methods are on the order of a few percentage or less and do not significantly impact
a resource assessment. The units of heat capacity are commonly given as kJ/kg-K or kJ/mole-K.
The heat capacity of a rock is determined by the minerals that compose the rock and the pore
space or fracture space that may or may not be fluid filled. Assuming that a rock has minimal frac-
ture or matrix porosity allows calculation of the approximate heat capacity of the rock. The heat
capacity of this solid component of the rock can be computed, approximately, as (assuming the units
of heat capacity are in kJ/kg-K)
C P rock = ∑ (x × w × C )/V , (7.3)
Pi
i
i
i
where C P rock is the heat capacity of the rock, x is the volume fraction of mineral i in the rock, w is
i
i
3
the molecular weight (kg/mole) of mineral i, V is the molar volume (m per mole) of i, and C is the
i
Pi
heat capacity of mineral i.
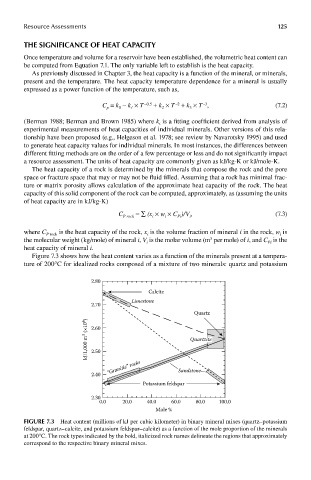
Figure 7.3 shows how the heat content varies as a function of the minerals present at a tempera-
ture of 200°C for idealized rocks composed of a mixture of two minerals: quartz and potassium
2.80
Calcite
Limestone
2.70
Quartz
kJ/1,000 m 3 (×10 6 ) 2.60 Quartzite

2.50
“Granitic” rocks Sandstone

2.40
Potassium feldspar

2.30
0.0 20.0 40.0 60.0 80.0 100.0
Mole %
FIGUre 7.3 Heat content (millions of kJ per cubic kilometer) in binary mineral mixes (quartz–potassium
feldspar, quartz–calcite, and potassium feldspar–calcite) as a function of the mole proportion of the minerals
at 200°C. The rock types indicated by the bold, italicized rock names delineate the regions that approximately
correspond to the respective binary mineral mixes.