Page 141 - Geothermal Energy Renewable Energy and The Environment

Resource Assessments 127

25
1 m/s

20

Pressure (MPa) 15 5 m/s 10 m/s

2 m/s
10

5
0 500 1000 1500 2000 2500
Distance (m)

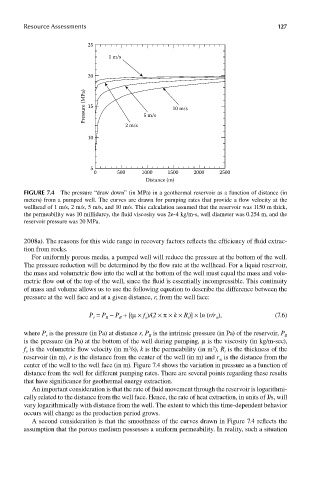
FIGUre 7.4 The pressure “draw down” (in MPa) in a geothermal reservoir as a function of distance (in
meters) from a pumped well. The curves are drawn for pumping rates that provide a flow velocity at the
wellhead of 1 m/s, 2 m/s, 5 m/s, and 10 m/s. This calculation assumed that the reservoir was 1150 m thick,
the permeability was 10 millidarcy, the fluid viscosity was 2e-4 kg/m-s, well diameter was 0.254 m, and the
reservoir pressure was 20 MPa.

2008a). The reasons for this wide range in recovery factors reflects the efficiency of fluid extrac-
tion from rocks.
For uniformly porous media, a pumped well will reduce the pressure at the bottom of the well.
The pressure reduction will be determined by the flow rate at the wellhead. For a liquid reservoir,
the mass and volumetric flow into the well at the bottom of the well must equal the mass and volu-
metric flow out of the top of the well, since the fluid is essentially incompressible. This continuity
of mass and volume allows us to use the following equation to describe the difference between the
pressure at the well face and at a given distance, r, from the well face:

P = P − P + [(μ × f )/(2 × π × k × R)] × ln (r/r ), (7.6)
R
w
r
v
B
t
where P is the pressure (in Pa) at distance r, P is the intrinsic pressure (in Pa) of the reservoir, P
R
B
r
is the pressure (in Pa) at the bottom of the well during pumping, μ is the viscosity (in kg/m-sec),
2
3
f is the volumetric flow velocity (in m /s), k is the permeability (in m ), R is the thickness of the
v
t
reservoir (in m), r is the distance from the center of the well (in m) and r is the distance from the
w
center of the well to the well face (in m). Figure 7.4 shows the variation in pressure as a function of
distance from the well for different pumping rates. There are several points regarding these results
that have significance for geothermal energy extraction.
An important consideration is that the rate of fluid movement through the reservoir is logarithmi-
cally related to the distance from the well face. Hence, the rate of heat extraction, in units of J/s, will
vary logarithmically with distance from the well. The extent to which this time-dependent behavior
occurs will change as the production period grows.
A second consideration is that the smoothness of the curves drawn in Figure 7.4 reflects the
assumption that the porous medium possesses a uniform permeability. In reality, such a situation