Page 142 - Geothermal Energy Renewable Energy and The Environment

128 Geothermal Energy: Renewable Energy and the Environment

1.0

0.8
Fraction of total flow 0.6 Dixie valley B-T model

0.4

0.2 Beowawe

0.0
0.0 0.2 0.4 0.6 0.8 1.0
Fraction of permeable volume
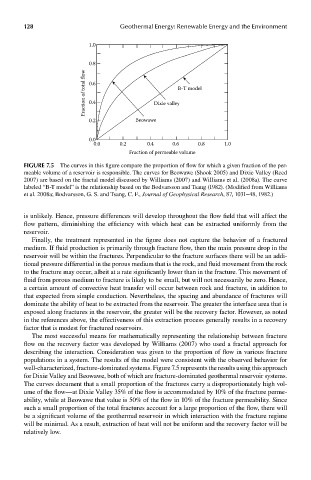
FIGUre 7.5 The curves in this figure compare the proportion of flow for which a given fraction of the per-
meable volume of a reservoir is responsible. The curves for Beowawe (Shook 2005) and Dixie Valley (Reed
2007) are based on the fractal model discussed by Williams (2007) and Williams et al. (2008a). The curve
labeled “B-T model” is the relationship based on the Bodvarsson and Tsang (1982). (Modified from Williams
et al. 2008a; Bodvarsson, G. S. and Tsang, C. F., Journal of Geophysical Research, 87, 1031–48, 1982.)

is unlikely. Hence, pressure differences will develop throughout the flow field that will affect the
flow pattern, diminishing the efficiency with which heat can be extracted uniformly from the
reservoir.
Finally, the treatment represented in the figure does not capture the behavior of a fractured
medium. If fluid production is primarily through fracture flow, then the main pressure drop in the
reservoir will be within the fractures. Perpendicular to the fracture surfaces there will be an addi-
tional pressure differential in the porous medium that is the rock, and fluid movement from the rock
to the fracture may occur, albeit at a rate significantly lower than in the fracture. This movement of
fluid from porous medium to fracture is likely to be small, but will not necessarily be zero. Hence,
a certain amount of convective heat transfer will occur between rock and fracture, in addition to
that expected from simple conduction. Nevertheless, the spacing and abundance of fractures will
dominate the ability of heat to be extracted from the reservoir. The greater the interface area that is
exposed along fractures in the reservoir, the greater will be the recovery factor. However, as noted
in the references above, the effectiveness of this extraction process generally results in a recovery
factor that is modest for fractured reservoirs.
The most successful means for mathematically representing the relationship between fracture
flow on the recovery factor was developed by Williams (2007) who used a fractal approach for
describing the interaction. Consideration was given to the proportion of flow in various fracture
populations in a system. The results of the model were consistent with the observed behavior for
well-characterized, fracture-dominated systems. Figure 7.5 represents the results using this approach
for Dixie Valley and Beowawe, both of which are fracture-dominated geothermal reservoir systems.
The curves document that a small proportion of the fractures carry a disproportionately high vol-
ume of the flow—at Dixie Valley 35% of the flow is accommodated by 10% of the fracture perme-
ability, while at Beowawe that value is 50% of the flow in 10% of the fracture permeability. Since
such a small proportion of the total fractures account for a large proportion of the flow, there will
be a significant volume of the geothermal reservoir in which interaction with the fracture regime
will be minimal. As a result, extraction of heat will not be uniform and the recovery factor will be
relatively low.