Page 74 - Geothermal Energy Renewable Energy and The Environment

58 Geothermal Energy: Renewable Energy and the Environment

10 1

10 –1
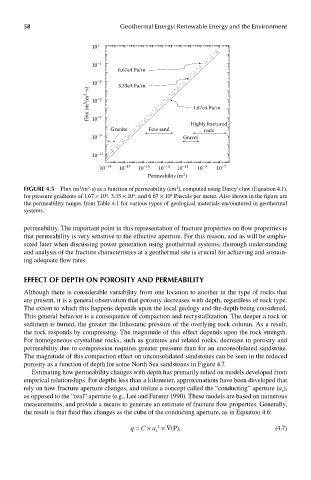
6.67e4 Pa/m
10 –3 3.33e4 Pa/m
Flux (m 3 /m 2 –s) 10 –5 1.67e4 Pa/m

–7
10
Highly fractured
Granite Fine sand rock
10 –9 Gravel
10 –11

10 –19 10 –17 10 –15 10 –13 10 –11 10 –9 10 –7
2
Permeability (m )
2
FIGUre 4.5 Flux (m /m -s) as a function of permeability (cm ), computed using Darcy’s law (Equation 4.1),
2
3
4
4
4
for pressure gradients of 1.67 × 10 , 3.33 × 10 , and 6.67 × 10 Pascals per meter. Also shown in the figure are
the permeability ranges from Table 4.1 for various types of geological materials encountered in geothermal
systems.
permeability. The important point in this representation of fracture properties on flow properties is
that permeability is very sensitive to the effective aperture. For this reason, and as will be empha-
sized later when discussing power generation using geothermal systems, thorough understanding
and analysis of the fracture characteristics at a geothermal site is crucial for achieving and sustain-
ing adequate flow rates.

eFFecT oF depTh on porosITy and permeabIlITy
Although there is considerable variability from one location to another in the type of rocks that
are present, it is a general observation that porosity decreases with depth, regardless of rock type.
The extent to which this happens depends upon the local geology and the depth being considered.
This general behavior is a consequence of compaction and recrystallization. The deeper a rock or
sediment is buried, the greater the lithostatic pressure of the overlying rock column. As a result,
the rock responds by compressing. The magnitude of this effect depends upon the rock strength.
For homogeneous crystalline rocks, such as granites and related rocks, decrease in porosity and
permeability due to compression requires greater pressure than for an unconsolidated sandstone.
The magnitude of this compaction effect on unconsolidated sandstones can be seen in the reduced
porosity as a function of depth for some North Sea sandstones in Figure 4.7.
Estimating how permeability changes with depth has primarily relied on models developed from
empirical relationships. For depths less than a kilometer, approximations have been developed that
rely on how fracture aperture changes, and utilize a concept called the “conducting” aperture (a ),
c
as opposed to the “real” aperture (e.g., Lee and Farmer 1990). These models are based on numerous
measurements, and provide a means to generate an estimate of fracture flow properties. Generally,
the result is that fluid flux changes as the cube of the conducting aperture, as in Equation 4.6:

q = C × a × ∇(P), (4.7)
3
c