Page 134 - Handbook of Electrical Engineering

116 HANDBOOK OF ELECTRICAL ENGINEERING

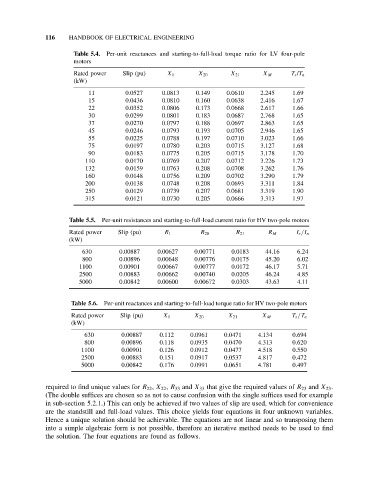
Table 5.4. Per-unit reactances and starting-to-full-load torque ratio for LV four-pole
motors
Rated power Slip (pu) X 1 X 20 X 21 X M T s /T n
(kW)
11 0.0527 0.0813 0.149 0.0610 2.245 1.69
15 0.0436 0.0810 0.160 0.0638 2.416 1.67
22 0.0352 0.0806 0.173 0.0668 2.617 1.66
30 0.0299 0.0801 0.183 0.0687 2.768 1.65
37 0.0270 0.0797 0.188 0.0697 2.863 1.65
45 0.0246 0.0793 0.193 0.0705 2.946 1.65
55 0.0225 0.0788 0.197 0.0710 3.023 1.66
75 0.0197 0.0780 0.203 0.0715 3.127 1.68
90 0.0183 0.0775 0.205 0.0715 3.178 1.70
110 0.0170 0.0769 0.207 0.0712 3.226 1.73
132 0.0159 0.0763 0.208 0.0708 3.262 1.76
160 0.0148 0.0756 0.209 0.0702 3.290 1.79
200 0.0138 0.0748 0.208 0.0693 3.311 1.84
250 0.0129 0.0739 0.207 0.0681 3.319 1.90
315 0.0121 0.0730 0.205 0.0666 3.313 1.97

Table 5.5. Per-unit resistances and starting-to-full-load current ratio for HV two-pole motors
Rated power Slip (pu) R 1 R 20 R 21 R M I s /I n
(kW)
630 0.00887 0.00627 0.00771 0.0183 44.16 6.24
800 0.00896 0.00648 0.00776 0.0175 45.20 6.02
1100 0.00901 0.00667 0.00777 0.0172 46.17 5.71
2500 0.00883 0.00662 0.00740 0.0205 46.24 4.85
5000 0.00842 0.00600 0.00672 0.0303 43.63 4.11

Table 5.6. Per-unit reactances and starting-to-full-load torque ratio for HV two-pole motors
Rated power Slip (pu) X 1 X 20 X 21 X M T s /T n
(kW)
630 0.00887 0.112 0.0961 0.0471 4.134 0.694
800 0.00896 0.118 0.0935 0.0470 4.313 0.620
1100 0.00901 0.126 0.0912 0.0477 4.518 0.550
2500 0.00883 0.151 0.0917 0.0537 4.817 0.472
5000 0.00842 0.176 0.0991 0.0651 4.781 0.497

required to find unique values for R 22 , X 22 , R 33 and X 33 that give the required values of R 23 and X 23 .
(The double suffices are chosen so as not to cause confusion with the single suffices used for example
in sub-section 5.2.1.) This can only be achieved if two values of slip are used, which for convenience
are the standstill and full-load values. This choice yields four equations in four unknown variables.
Hence a unique solution should be achievable. The equations are not linear and so transposing them
into a simple algebraic form is not possible, therefore an iterative method needs to be used to find
the solution. The four equations are found as follows.