Page 63 - Handbook of Electrical Engineering

42 HANDBOOK OF ELECTRICAL ENGINEERING

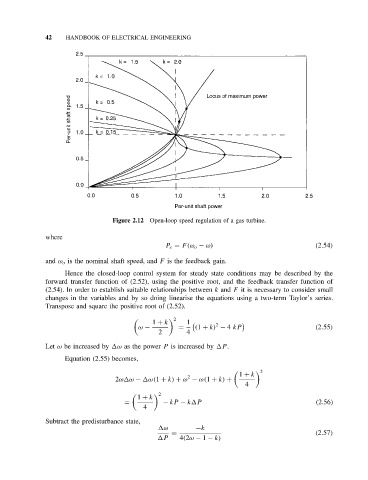
Figure 2.12 Open-loop speed regulation of a gas turbine.
where
P e = F(ω o − ω) (2.54)

and ω o is the nominal shaft speed, and F is the feedback gain.
Hence the closed-loop control system for steady state conditions may be described by the
forward transfer function of (2.52), using the positive root, and the feedback transfer function of
(2.54). In order to establish suitable relationships between k and F it is necessary to consider small
changes in the variables and by so doing linearise the equations using a two-term Taylor’s series.
Transpose and square the positive root of (2.52).

2

1 + k 1 2
ω − = (1 + k) − 4 kP (2.55)
2 4
Let ω be increased by ω as the power P is increased by P .
Equation (2.55) becomes,
2

1 + k
2
2ω ω − ω(1 + k) + ω − ω(1 + k) +
4
2
1 + k

= − kP − k P (2.56)
4
Subtract the predisturbance state,
ω −k
= (2.57)
P 4(2ω − 1 − k)