Page 172 - Hardware Implementation of Finite-Field Arithmetic

m
Operations over GF ( p ) 155

if R(S-1-I) = 1 then E := Product_Mod_F(E, H, F);
end if;
end loop;
A := Product_Mod_F(E, H, F);
E := Product(E, Invert(A(0)));
Z := Product_Mod_F(E, G, F);
An executable Ada file reduction_to_multiplications.adb, including
Algorithm 6.6 is available at www.arithmetic-circuits.org.
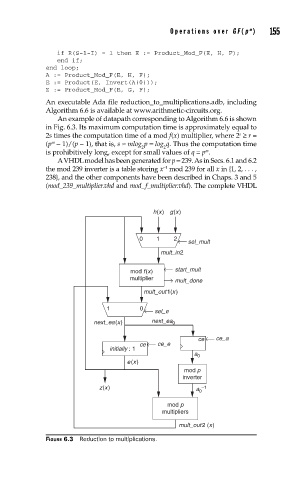
An example of datapath corresponding to Algorithm 6.6 is shown
in Fig. 6.3. Its maximum computation time is approximately equal to
2s times the computation time of a mod f(x) multiplier, where 2 ≥ r =
s
m
(p − 1)/(p − 1), that is, s ≈ mlog p = log q. Thus the computation time
2 2
m
is prohibitively long, except for small values of q = p .
A VHDL model has been generated for p = 239. As in Secs. 6.1 and 6.2
−1
the mod 239 inverter is a table storing x mod 239 for all x in {1, 2, . . . ,
238}, and the other components have been described in Chaps. 3 and 5
(mod_239_multiplier.vhd and mod_ f_multiplier.vhd). The complete VHDL
h(x) g(x)

0 1 2
sel_mult
mult_in2

mod f(x) start_mult
multiplier
mult_done
mult_out1(x)

1 0
sel_e
next_ea(x) next_ea 0
ce ce_a
ce ce_e
initially : 1
a 0
e(x)
mod p
inverter
z(x) a 0 –1

mod p
multipliers
mult_out 2 (x)

FIGURE 6.3 Reduction to multiplications.