Page 196 - Innovations in Intelligent Machines

188 R.W. Beard
50

0
φ (deg)
actual
- 50
estimated
- 100
0 5 10 15 20 25 30

150

100
θ (deg) actual
50 estimated

0

- 50
0 5 10 15 20 25 30
time (sec)
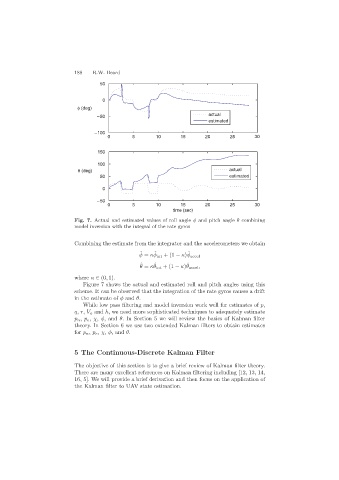
Fig. 7. Actual and estimated values of roll angle φ and pitch angle θ combining
model inversion with the integral of the rate gyros

Combining the estimate from the integrator and the accelerometers we obtain
ˆ ˆ ˆ
φ = κφ int +(1 − κ)φ accel
ˆ
ˆ
ˆ
θ = κθ int +(1 − κ)θ accel ,
where κ ∈ (0, 1).
Figure 7 shows the actual and estimated roll and pitch angles using this
scheme. It can be observed that the integration of the rate gyros causes a drift
in the estimate of φ and θ.
While low pass filtering and model inversion work well for estimates of p,
q, r, V a and h, we need more sophisticated techniques to adequately estimate
p n , p e , χ, φ,and θ. In Section 5 we will review the basics of Kalman filter
theory. In Section 6 we use two extended Kalman filters to obtain estimates
for p n , p e , χ, φ,and θ.

5 The Continuous-Discrete Kalman Filter

The objective of this section is to give a brief review of Kalman filter theory.
There are many excellent references on Kalman filtering including [12, 13, 14,
16, 5]. We will provide a brief derivation and then focus on the application of
the Kalman filter to UAV state estimation.