Page 180 - Intro to Tensor Calculus

175

VECTOR GENERAL TENSOR CARTESIAN TENSOR

i
~
A A or A i A i
~ ~
i
j
i
A · B A B i = g ij A B = A i B i A i B i
i ij
A B i = g A i B j
1 ijk
~
~
i
~
C = A × B C = √ e A j B k C i = e ijk A j B k
g
∂Φ
im
∇ Φ = grad Φ g Φ ,m Φ ,i =
∂x i
1 ∂ √ r ∂A i
~
mn
r
~
∇· A = div A g A m,n = A ,r = √ ( gA ) A i,i =
g ∂x r ∂x i
~
~
~
i
∇× A = C =curl A C = ijk A k,j C i = e ijk ∂A k
∂x j
1 ∂ √ ij ∂U ∂ ∂U
mn
2
∇ U g U ,mn = √ gg
g ∂x j ∂x i ∂x i ∂x i
m
i
~
~
~
C =(A ·∇)B C = A B i ∂B i
,m C i = A m m
∂x
~
~
i
i
~
C = A(∇· B) C = A B j ,j C i = A i ∂B m
∂x m
∂ ∂A i
2 ~
~
jm
jm
i
i
C = ∇ A C = g A ,mj or C i = g A i,mj C i =
∂x m ∂x m
im i
~
A ·∇ φ g A φ ,m A i φ ,i
2
∂ A r
~
∇ ∇· A g im A r
,r ,m
∂x i ∂x r
2 2
∂ A j ∂ A i
~
∇× ∇× A ijk g jm kst A t,s −
,m
∂x j ∂x i ∂x j ∂x j
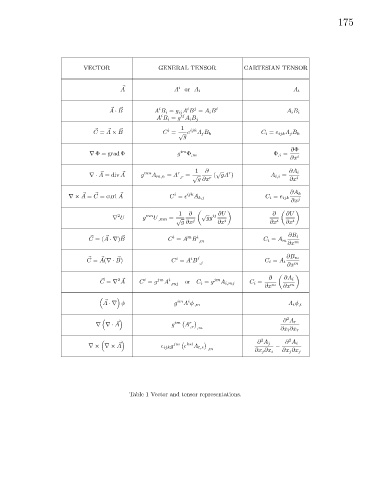
Table 1 Vector and tensor representations.