Page 243 - Introduction to Autonomous Mobile Robots

228

System error Chapter 5
source

Control System

System state
(desired but
not known)

Observed Optimal estimate
Measuring measurement Kalman of system state
devices filter

Measurement
error sources

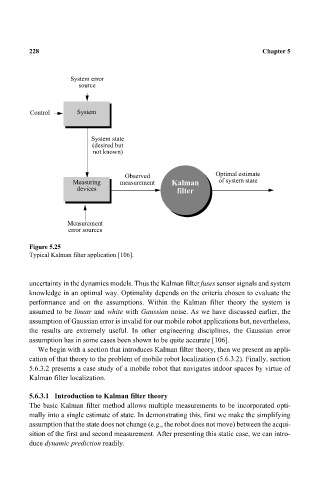
Figure 5.25
Typical Kalman filter application [106].

uncertainty in the dynamics models. Thus the Kalman filter fuses sensor signals and system
knowledge in an optimal way. Optimality depends on the criteria chosen to evaluate the
performance and on the assumptions. Within the Kalman filter theory the system is
assumed to be linear and white with Gaussian noise. As we have discussed earlier, the
assumption of Gaussian error is invalid for our mobile robot applications but, nevertheless,
the results are extremely useful. In other engineering disciplines, the Gaussian error
assumption has in some cases been shown to be quite accurate [106].
We begin with a section that introduces Kalman filter theory, then we present an appli-
cation of that theory to the problem of mobile robot localization (5.6.3.2). Finally, section
5.6.3.2 presents a case study of a mobile robot that navigates indoor spaces by virtue of
Kalman filter localization.

5.6.3.1 Introduction to Kalman filter theory
The basic Kalman filter method allows multiple measurements to be incorporated opti-
mally into a single estimate of state. In demonstrating this, first we make the simplifying
assumption that the state does not change (e.g., the robot does not move) between the acqui-
sition of the first and second measurement. After presenting this static case, we can intro-
duce dynamic prediction readily.