Page 115 - Introduction to Computational Fluid Dynamics

P1: IWV
11:7
May 25, 2005
0521853265c04
94
1E-2 CB908/Date 0 521 85326 5 1E-2 2D BOUNDARY LAYERS
−0.5 −0.2
Cfx = 0.664 Rex Cfx = 0.0574 Rex
−0.5 −0.2
Stx = 0.42 Rex Stx = 0.0331 Rex
Cfx
Stx
LOW Re
1E-3 MODEL 1E-3
LOW Re
MODEL
MIXING LENGTH
MODEL
Pr = 0.7 MIXING LENGTH
MODEL
Rex Rex
1E-4 1E-4
1E5 1E6 1E7 1E5 1E6 1E7
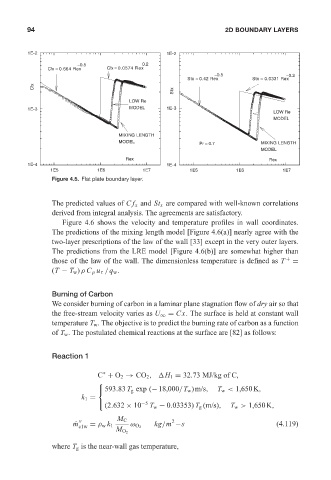
Figure 4.5. Flat plate boundary layer.

The predicted values of Cf x and St x are compared with well-known correlations
derived from integral analysis. The agreements are satisfactory.
Figure 4.6 shows the velocity and temperature profiles in wall coordinates.
The predictions of the mixing length model [Figure 4.6(a)] nearly agree with the
two-layer prescriptions of the law of the wall [33] except in the very outer layers.
The predictions from the LRE model [Figure 4.6(b)] are somewhat higher than
those of the law of the wall. The dimensionless temperature is defined as T + =
(T − T w )ρ C p u τ /q w .

Burning of Carbon
We consider burning of carbon in a laminar plane stagnation flow of dry air so that
the free-stream velocity varies as U ∞ = Cx. The surface is held at constant wall
temperature T w . The objective is to predict the burning rate of carbon as a function
of T w . The postulated chemical reactions at the surface are [82] as follows:

Reaction 1

∗
C + O 2 → CO 2 , H 1 = 32.73 MJ/kg of C,
⎧
⎨ 593.83 T g exp (−18,000/T w )m/s, T w < 1,650K,
k 1 =
(2.632 × 10 T w − 0.03353) T g (m/s), T w > 1,650K,
⎩ −5
M C 2
˙ m = ρ w k 1 kg/m −s (4.119)
c1w ω O 2
M O 2
where T g is the near-wall gas temperature,