Page 119 - Introduction to Computational Fluid Dynamics

P1: IWV
11:7
May 25, 2005
CB908/Date
0521853265c04
98
1.2 0 521 85326 5 2D BOUNDARY LAYERS
Solid Line - With Reaction 1
H O = 0.001
2
1.0 Dashed Line - Without Reaction 1
Sc = 0.51
P = 0.72 BRR (PRED)
r
0.8
0.6
BRR (EXPT)
0.4 O 2
CO 2
0.2 CO

0.0

−0.2
800 1000 1200 1400 1600 1800
Tw
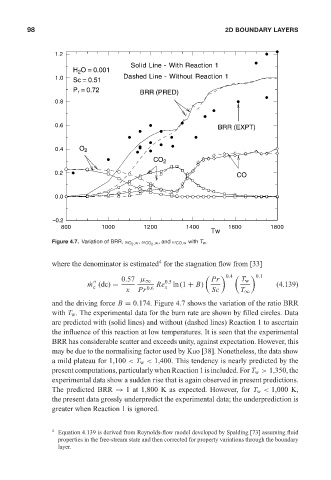
Figure 4.7. Variation of BRR, ω O 2 ,w , ω CO 2 ,w , and ω CO,w with T w .

4
where the denominator is estimated for the stagnation flow from [33]
0.4 0.1
Pr
0.57 µ ∞ 0.5 T w
˙ m (dc) = Re ln(1 + B) (4.139)
c 0.6 x
x Pr Sc T ∞
and the driving force B = 0.174. Figure 4.7 shows the variation of the ratio BRR
with T w . The experimental data for the burn rate are shown by filled circles. Data
are predicted with (solid lines) and without (dashed lines) Reaction 1 to ascertain
the influence of this reaction at low temperatures. It is seen that the experimental
BRR has considerable scatter and exceeds unity, against expectation. However, this
may be due to the normalising factor used by Kuo [38]. Nonetheless, the data show
a mild plateau for 1,100 < T w < 1,400. This tendency is nearly predicted by the
present computations, particularly when Reaction 1 is included. For T w > 1,350, the
experimental data show a sudden rise that is again observed in present predictions.
The predicted BRR → 1 at 1,800 K as expected. However, for T w < 1,000 K,
the present data grossly underpredict the experimental data; the underprediction is
greater when Reaction 1 is ignored.

4 Equation 4.139 is derived from Reynolds-flow model developed by Spalding [73] assuming fluid
properties in the free-stream state and then corrected for property variations through the boundary
layer.