Page 176 - Introduction to Computational Fluid Dynamics

P1: IWV
0 521 85326 5
CB908/Date
0521853265c05
EXERCISES
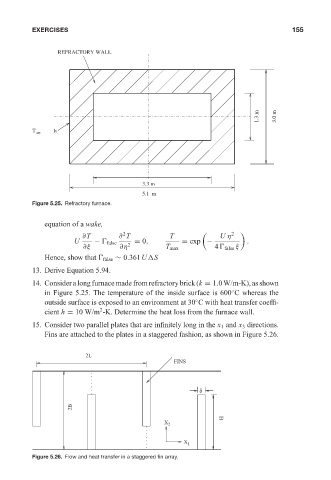
REFRACTORY WALL May 20, 2005 12:28 155

1.3 m 3.0 m

T h
8

3.3 m
5.1 m
Figure 5.25. Refractory furnace.

equation of a wake,
2
∂T ∂ T T U η 2
U −
false = 0, = exp − .
∂ξ ∂η 2 T max 4
false ξ
Hence, show that
false ∼ 0.361U S
13. Derive Equation 5.94.
14. Consideralongfurnacemadefromrefractorybrick(k = 1.0W/m-K),asshown
◦
in Figure 5.25. The temperature of the inside surface is 600 C whereas the
◦
outside surface is exposed to an environment at 30 C with heat transfer coeffi-
2
cient h = 10 W/m -K. Determine the heat loss from the furnace wall.
15. Consider two parallel plates that are infinitely long in the x 1 and x 3 directions.
Fins are attached to the plates in a staggered fashion, as shown in Figure 5.26.

2L
FINS

δ

2B
H
X 2

X 1
Figure 5.26. Flow and heat transfer in a staggered fin array.