Page 95 - Introduction to chemical reaction engineering and kinetics

4.3 Dependence of Rate on Concentration 77

0.9
0.8

0.6
0
e 0 5
z
0.4
0.3
0.2
0 . 1

1 2 3 4 5 6 7 8 9 1
MAn
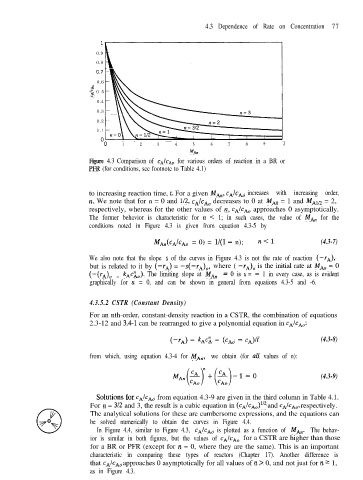
Figure 4.3 Comparison of CAICA~ for various orders of reaction in a BR or
PP’R (for conditions, see footnote to Table 4.1)

to increasing reaction time, t. For a given MA”, cA/cAO increases with increasing order,
n. We note that for IZ = 0 and 1/2, cAIcAO decreases to 0 at MA0 = 1 and MAn2 = 2,
respectively, whereas for the other values of IZ, cAIcAO approaches 0 asymptotically.
The former behavior is characteristic for IZ < 1; in such cases, the value of MA,, for the
conditions noted in Figure 4.3 is given from equation 4.3-5 by

MAACdCh = 0) = l/(l - n); n<l (4.3-7)

We also note that the slope s of the curves in Figure 4.3 is not the rate of reaction (-Y*),
but is related to it by (-rA) = -s(--I*)~, where ( --I*)~ is the initial rate at MAn = 0
). The limiting slope at MA,, = 0 is s = - 1 in every case, as is evident
(-@Ah = kAcko
graphically for n = 0, and can be shown in general from equations 4.3-5 and -6.

4.3.5.2 CSTR (Constant Density)

For an nth-order, constant-density reaction in a CSTR, the combination of equations
2.3-12 and 3.4-1 can be rearranged to give a polynomial equation in cA/cAO:

(-TA) = kAc1 = (CA0 - c&t (4.3-8)

from which, using equation 4.3-4 for MA", we obtain (for all values of n):

(4.3-9)

SOhltiOllS for CA/CA0 from equation 4.3-9 are given in the third column in Table 4.1.
For II = 312 and 3, the result is a cubic equation in (cA/cAo)lc! and CA/CA~, respectively.
The analytical solutions for these are cumbersome expressions, and the equations can
be solved numerically to obtain the curves in Figure 4.4.
In Figure 4.4, similar to Figure 4.3, CA/CA~ is plotted as a function of MA,,. The behav-
ior is similar in both figures, but the values of CA/CA~ for a CSTR are higher than those
for a BR or PFR (except for n = 0, where they are the same). This is an important
characteristic in comparing these types of reactors (Chapter 17). Another difference is
that CA/CA~ approaches 0 asymptotically for all values of n > 0, and not just for it 2 1,
as in Figure 4.3.