Page 152 - Marks Calculation for Machine Design

P1: Rakesh
January 4, 2005
14:16
Brown.cls
Brown˙C03
134
p STRENGTH OF MACHINES p o
o
s
p r t p
i i i
r i
s a s a
s
r t
r o o
Front view Side view
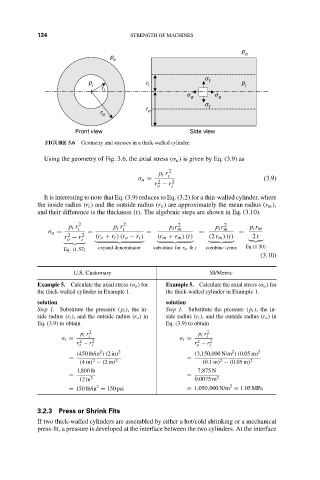
FIGURE 3.6 Geometry and stresses in a thick-walled cylinder.
Using the geometry of Fig. 3.6, the axial stress (σ a ) is given by Eq. (3.9) as
p i r i 2
σ a = 2 2 (3.9)
r − r i
o
It is interesting to note that Eq. (3.9) reduces to Eq. (3.2) for a thin-walled cylinder, where
the inside radius (r i ) and the outside radius (r o ) are approximately the mean radius (r m ),
and their difference is the thickness (t). The algebraic steps are shown in Eq. (3.10).
p i r i 2 p i r i 2 p i r 2 m p i r m 2 p i r m
σ a = 2 2 = = = =
r − r i (r o + r i )(r o − r i ) (r m + r m )(t) (2r m )(t) 2 t
o

expand denominator substitute for r m & t combine terms Eq.(1.50)
Eq.(1.57)
(3.10)
U.S. Customary SI/Metric
Example 5. Calculate the axial stress (σ a ) for Example 5. Calculate the axial stress (σ a ) for
the thick-walled cylinder in Example 1. the thick-walled cylinder in Example 1.
solution solution
Step 1. Substitute the pressure (p i ), the in- Step 1. Substitute the pressure (p i ), the in-
side radius (r i ), and the outside radius (r o ) in side radius (r i ), and the outside radius (r o ) in
Eq. (3.9) to obtain Eq. (3.9) to obtain
p i r 2 p i r 2
σ t = i 2 σ t = i 2
2
2
r − r i r − r i
o
o
2
2
(450 lb/in )(2in) 2 (3,150,000 N/m )(0.05 m) 2
= =
2
2
(4in) − (2in) 2 (0.1m) − (0.05 m) 2
1,800 lb 7,875 N
= =
12 in 2 0.0075 m 2
2
2
= 150 lb/in = 150 psi = 1,050,000 N/m = 1.05 MPa
3.2.3 Press or Shrink Fits
If two thick-walled cylinders are assembled by either a hot/cold shrinking or a mechanical
press-fit, a pressure is developed at the interface between the two cylinders. At the interface