Page 255 - Marks Calculation for Machine Design

P1: Shibu
14:56
January 4, 2005
Brown.cls
Brown˙C06
237
STATIC DESIGN AND COLUMN BUCKLING
minimum principal stress (σ 2 ). Also, combinations in the third (III) quadrant require that
the minimum principal stress (σ 2 ) be at least equal to or more negative than the maximum
principal stress (σ 1 ).
The factor-of-safety (n) for this theory is given in Eq. (6.6), which replaces the inequality
sign in Eq. (6.5) with an equal to sign, then rearranged to give
σ 1 − σ 2 1
= (6.6)
S y n
An alternate expression commonly used in place of Eq. (6.6) for the factor-of-safety (n)
for the maximum-shear-stress theory can be defined using the maximum shear stress (τ max )
and the yield strength in shear (S sy ) from Eq. (6.4) as
τ max 1
= (6.7)
S sy n
Distortion-Energy Theory. Without presenting the many steps in its development that
can be found in any number of references, the expression given in Eq. (6.8) represents the
combinations of the principal stresses (σ 1 , σ 2 ) for a safe design according to the distortion-
energy theory.
2
2
σ + σ − σ 1 σ 2 < S 2 y (6.8)
2
1
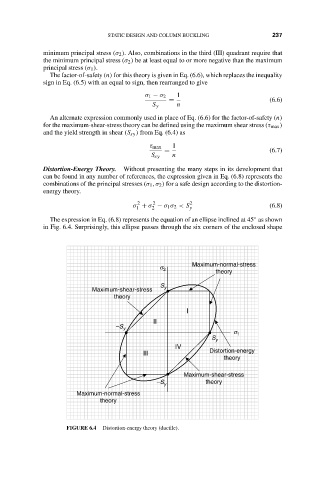
The expression in Eq. (6.8) represents the equation of an ellipse inclined at 45 as shown
◦
in Fig. 6.4. Surprisingly, this ellipse passes through the six corners of the enclosed shape
Maximum-normal-stress
s 2
theory
S y
Maximum-shear-stress
theory

I
II
–S y
s 1
S y
IV
III Distortion-energy
theory
Maximum-shear-stress
–S y theory
Maximum-normal-stress
theory

FIGURE 6.4 Distortion-energy theory (ductile).