Page 256 - Marks Calculation for Machine Design

P1: Shibu
January 4, 2005
14:56
Brown.cls
Brown˙C06
STRENGTH OF MACHINES
238
showninFig. 6.3,whichisacombinationofthe maximum-normal-stress theoryin quadrants
(I) and (III) and the maximum-shear-stress theory in quadrants (II) and (IV).
The factor-of-safety (n) for this theory is given in Eq. (6.9), which replaces the inequality
sign in Eq. (6.8) with an equal to sign and is then rearranged to give
1/2
2 2

σ + σ − σ 1 σ 2 1
1 2
= (6.9)
S y n
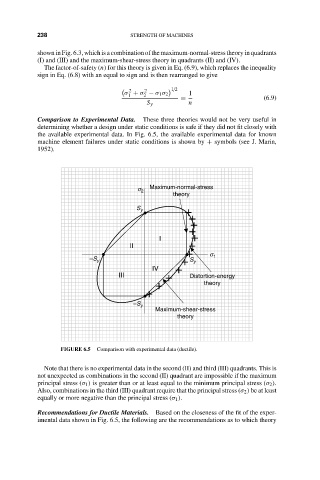
Comparison to Experimental Data. These three theories would not be very useful in
determining whether a design under static conditions is safe if they did not fit closely with
the available experimental data. In Fig. 6.5, the available experimental data for known
machine element failures under static conditions is shown by + symbols (see J. Marin,
1952).
s 2 Maximum-normal-stress
theory
S y +
+
+
+
I +
II +
+ s
–S y + S y 1
IV +
III + Distortion-energy
+ theory
+
–S y
Maximum-shear-stress
theory

FIGURE 6.5 Comparison with experimental data (ductile).

Note that there is no experimental data in the second (II) and third (III) quadrants. This is
not unexpected as combinations in the second (II) quadrant are impossible if the maximum
principal stress (σ 1 ) is greater than or at least equal to the minimum principal stress (σ 2 ).
Also, combinations in the third (III) quadrant require that the principal stress (σ 2 ) be at least
equally or more negative than the principal stress (σ 1 ).

Recommendations for Ductile Materials. Based on the closeness of the fit of the exper-
imental data shown in Fig. 6.5, the following are the recommendations as to which theory