Page 213 - Materials Science and Engineering An Introduction

6.6 Tensile Properties • 185

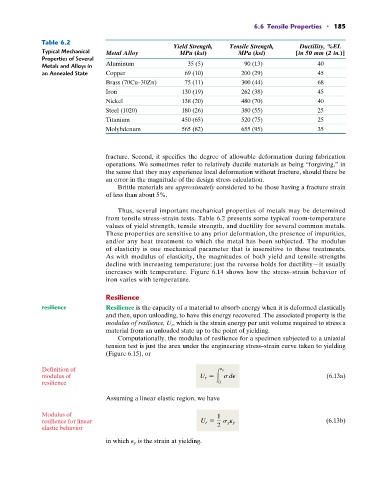
Table 6.2
Yield Strength, Tensile Strength, Ductility, %EL
Typical Mechanical Metal Alloy MPa (ksi) MPa (ksi) [in 50 mm (2 in.)]
Properties of Several
Metals and Alloys in Aluminum 35 (5) 90 (13) 40
an Annealed State Copper 69 (10) 200 (29) 45
Brass (70Cu–30Zn) 75 (11) 300 (44) 68
Iron 130 (19) 262 (38) 45
Nickel 138 (20) 480 (70) 40
Steel (1020) 180 (26) 380 (55) 25
Titanium 450 (65) 520 (75) 25
Molybdenum 565 (82) 655 (95) 35

fracture. Second, it specifies the degree of allowable deformation during fabrication
operations. We sometimes refer to relatively ductile materials as being “forgiving,” in
the sense that they may experience local deformation without fracture, should there be
an error in the magnitude of the design stress calculation.
Brittle materials are approximately considered to be those having a fracture strain
of less than about 5%.

Thus, several important mechanical properties of metals may be determined
from tensile stress–strain tests. Table 6.2 presents some typical room-temperature
values of yield strength, tensile strength, and ductility for several common metals.
These properties are sensitive to any prior deformation, the presence of impurities,
and/or any heat treatment to which the metal has been subjected. The modulus
of elasticity is one mechanical parameter that is insensitive to these treatments.
As with modulus of elasticity, the magnitudes of both yield and tensile strengths
decline with increasing temperature; just the reverse holds for ductility—it usually
increases with temperature. Figure 6.14 shows how the stress–strain behavior of
iron varies with temperature.

Resilience
resilience Resilience is the capacity of a material to absorb energy when it is deformed elastically
and then, upon unloading, to have this energy recovered. The associated property is the
modulus of resilience, U r , which is the strain energy per unit volume required to stress a
material from an unloaded state up to the point of yielding.
Computationally, the modulus of resilience for a specimen subjected to a uniaxial
tension test is just the area under the engineering stress–strain curve taken to yielding
(Figure 6.15), or

Definition of P y
modulus of U r = 3 s dP (6.13a)
resilience 0

Assuming a linear elastic region, we have

Modulus of 1
resilience for linear U r = s y P y (6.13b)
elastic behavior 2
in which P y is the strain at yielding.