Page 250 - Materials Science and Engineering An Introduction

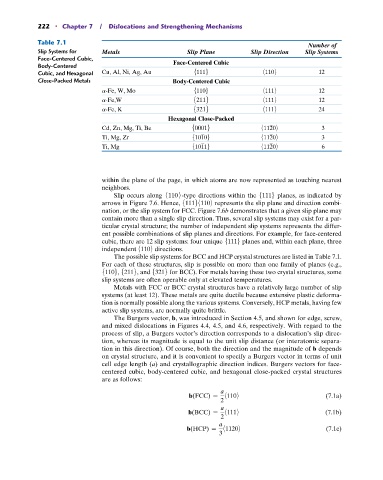
222 • Chapter 7 / Dislocations and Strengthening Mechanisms

Table 7.1
Number of
Slip Systems for Metals Slip Plane Slip Direction Slip Systems
Face-Centered Cubic,
Body-Centered Face-Centered Cubic
Cubic, and Hexagonal Cu, Al, Ni, Ag, Au 51116 81109 12
Close-Packed Metals Body-Centered Cubic
a-Fe, W, Mo 51106 81119 12
a-Fe,W 52116 81119 12
a-Fe, K 53216 81119 24
Hexagonal Close-Packed
Cd, Zn, Mg, Ti, Be 500016 811209 3
Ti, Mg, Zr 510106 811209 3
Ti, Mg 510116 811209 6

within the plane of the page, in which atoms are now represented as touching nearest
neighbors.
Slip occurs along 81109-type directions within the 51116 planes, as indicated by
arrows in Figure 7.6. Hence, 5111681109 represents the slip plane and direction combi-
nation, or the slip system for FCC. Figure 7.6b demonstrates that a given slip plane may
contain more than a single slip direction. Thus, several slip systems may exist for a par-
ticular crystal structure; the number of independent slip systems represents the differ-
ent possible combinations of slip planes and directions. For example, for face-centered
cubic, there are 12 slip systems: four unique 51116 planes and, within each plane, three
independent 81109 directions.
The possible slip systems for BCC and HCP crystal structures are listed in Table 7.1.
For each of these structures, slip is possible on more than one family of planes (e.g.,
51106, 52116, and 53216 for BCC). For metals having these two crystal structures, some
slip systems are often operable only at elevated temperatures.
Metals with FCC or BCC crystal structures have a relatively large number of slip
systems (at least 12). These metals are quite ductile because extensive plastic deforma-
tion is normally possible along the various systems. Conversely, HCP metals, having few
active slip systems, are normally quite brittle.
The Burgers vector, b, was introduced in Section 4.5, and shown for edge, screw,
and mixed dislocations in Figures 4.4, 4.5, and 4.6, respectively. With regard to the
process of slip, a Burgers vector’s direction corresponds to a dislocation’s slip direc-
tion, whereas its magnitude is equal to the unit slip distance (or interatomic separa-
tion in this direction). Of course, both the direction and the magnitude of b depends
on crystal structure, and it is convenient to specify a Burgers vector in terms of unit
cell edge length (a) and crystallographic direction indices. Burgers vectors for face-
centered cubic, body-centered cubic, and hexagonal close-packed crystal structures
are as follows:

a
b(FCC) = 81109 (7.1a)

2
a
b(BCC) = 81119 (7.1b)

2
a
b(HCP) = 811209 (7.1c)

3