Page 187 - Mathematical Models and Algorithms for Power System Optimization

178 Chapter 6

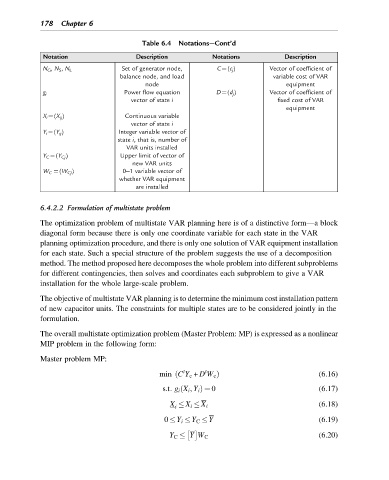
Table 6.4 Notations—Cont’d
Notation Description Notations Description

Set of generator node, C¼(c j ) Vector of coefficient of
N G , N S , N L
balance node, and load variable cost of VAR
node equipment
g i Power flow equation D¼(d j ) Vector of coefficient of
vector of state i fixed cost of VAR
equipment
X i ¼(X ij ) Continuous variable
vector of state i
Y i ¼(Y ij ) Integer variable vector of
state i, that is, number of
VAR units installed
Y C ¼(Y Cj ) Upper limit of vector of
new VAR units
W C ¼(W Cj ) 0–1 variable vector of
whether VAR equipment
are installed

6.4.2.2 Formulation of multistate problem
The optimization problem of multistate VAR planning here is of a distinctive form—a block
diagonal form because there is only one coordinate variable for each state in the VAR
planning optimization procedure, and there is only one solution of VAR equipment installation
for each state. Such a special structure of the problem suggests the use of a decomposition
method. The method proposed here decomposes the whole problem into different subproblems
for different contingencies, then solves and coordinates each subproblem to give a VAR
installation for the whole large-scale problem.

The objective of multistate VAR planning is to determine the minimum cost installation pattern
of new capacitor units. The constraints for multiple states are to be considered jointly in the
formulation.
The overall multistate optimization problem (Master Problem: MP) is expressed as a nonlinear
MIP problem in the following form:

Master problem MP:
t t
ð
min C Y c + D W c Þ (6.16)
s:t: g i X i , Y i Þ ¼ 0 (6.17)
ð
(6.18)
X X i X i
i
0 Y i Y C Y (6.19)

Y C Y W C (6.20)