Page 225 - Mathematical Models and Algorithms for Power System Optimization

216 Chapter 6

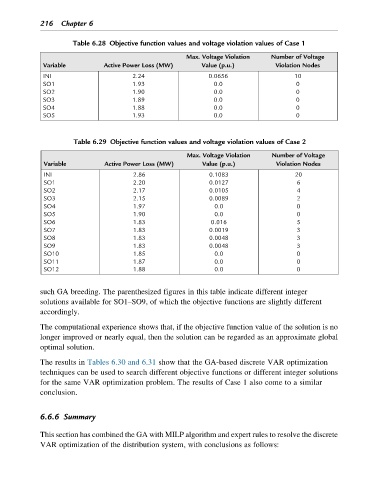
Table 6.28 Objective function values and voltage violation values of Case 1
Max. Voltage Violation Number of Voltage
Variable Active Power Loss (MW) Value (p.u.) Violation Nodes

INI 2.24 0.0656 10
SO1 1.93 0.0 0
SO2 1.90 0.0 0
SO3 1.89 0.0 0
SO4 1.88 0.0 0
SO5 1.93 0.0 0

Table 6.29 Objective function values and voltage violation values of Case 2
Max. Voltage Violation Number of Voltage
Variable Active Power Loss (MW) Value (p.u.) Violation Nodes

INI 2.86 0.1083 20
SO1 2.20 0.0127 6
SO2 2.17 0.0105 4
SO3 2.15 0.0089 2
SO4 1.97 0.0 0
SO5 1.90 0.0 0
SO6 1.83 0.016 5
SO7 1.83 0.0019 3
SO8 1.83 0.0048 3
SO9 1.83 0.0048 3
SO10 1.85 0.0 0
SO11 1.87 0.0 0
SO12 1.88 0.0 0

such GA breeding. The parenthesized figures in this table indicate different integer
solutions available for SO1–SO9, of which the objective functions are slightly different
accordingly.
The computational experience shows that, if the objective function value of the solution is no
longer improved or nearly equal, then the solution can be regarded as an approximate global
optimal solution.
The results in Tables 6.30 and 6.31 show that the GA-based discrete VAR optimization
techniques can be used to search different objective functions or different integer solutions
for the same VAR optimization problem. The results of Case 1 also come to a similar
conclusion.

6.6.6 Summary

This section has combined the GA with MILP algorithm and expert rules to resolve the discrete
VAR optimization of the distribution system, with conclusions as follows: