Page 226 - Mathematical Models and Algorithms for Power System Optimization

Discrete Optimization for Reactive Power Planning 217

SO9 1 3 (1) 4 1 (4) 1 3 1 5 6 4 1 4 6 (4) 1 1

SO9 1 3 (1) 4 1 (4) 1 3 1 5 6 4 1 4 6 (4) 1 1

SO8 1 3 2 (5) 1 (4) 1 3 1 5 6 4 1 4 6 (4) 1 1

2
Case

in SO7 1 3 2 (5) 1 (4) 1 3 1 5 6 4 1 4 6 5 1 1
ratio

tap SO7 1 3 (1) 4 1 (4) 1 3 1 5 6 4 1 4 6 5 1 1
of
constraints SO6 1 3 2 4 1 (4) 1 3 1 5 6 4 1 4 6# 5" 1 1

and SO5 1 3 (3) 4 1 3 1 3 1 (6) 6 4 2 4 5 6 1 1
solutions

Integer SO4 1 3 2 4 1 3 1 3 1 (6) (7) 4 2 4 5 6 1 1

6.30 SO3 1 3 2 4 1 3 1 3 1 (6) (7) 4 2 4 5 6 1 1

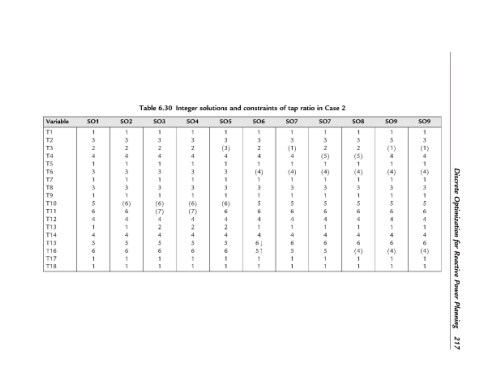
Table

SO2 1 3 2 4 1 3 1 3 1 (6) 6 4 1 4 5 6 1 1

SO1 1 3 2 4 1 3 1 3 1 5 6 4 1 4 5 6 1 1

Variable T1 T2 T3 T4 T5 T6 T7 T8 T9 T10 T11 T12 T13 T14 T15 T16 T17 T18