Page 227 - Mathematical Models and Algorithms for Power System Optimization

218 Chapter 6

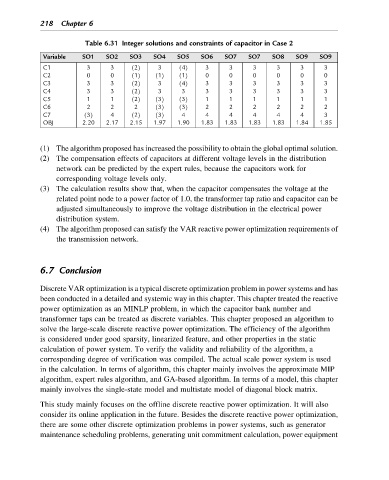
Table 6.31 Integer solutions and constraints of capacitor in Case 2
Variable SO1 SO2 SO3 SO4 SO5 SO6 SO7 SO7 SO8 SO9 SO9

C1 3 3 (2) 3 (4) 3 3 3 3 3 3
C2 0 0 (1) (1) (1) 0 0 0 0 0 0
C3 3 3 (2) 3 (4) 3 3 3 3 3 3
C4 3 3 (2) 3 3 3 3 3 3 3 3
C5 1 1 (2) (3) (3) 1 1 1 1 1 1
C6 2 2 2 (3) (3) 2 2 2 2 2 2
C7 (3) 4 (2) (3) 4 4 4 4 4 4 3
OBJ 2.20 2.17 2.15 1.97 1.90 1.83 1.83 1.83 1.83 1.84 1.85

(1) The algorithm proposed has increased the possibility to obtain the global optimal solution.
(2) The compensation effects of capacitors at different voltage levels in the distribution
network can be predicted by the expert rules, because the capacitors work for
corresponding voltage levels only.
(3) The calculation results show that, when the capacitor compensates the voltage at the
related point node to a power factor of 1.0, the transformer tap ratio and capacitor can be
adjusted simultaneously to improve the voltage distribution in the electrical power
distribution system.
(4) The algorithm proposed can satisfy the VAR reactive power optimization requirements of
the transmission network.

6.7 Conclusion

Discrete VAR optimization is a typical discrete optimization problem in power systems and has
been conducted in a detailed and systemic way in this chapter. This chapter treated the reactive
power optimization as an MINLP problem, in which the capacitor bank number and
transformer taps can be treated as discrete variables. This chapter proposed an algorithm to
solve the large-scale discrete reactive power optimization. The efficiency of the algorithm
is considered under good sparsity, linearized feature, and other properties in the static
calculation of power system. To verify the validity and reliability of the algorithm, a
corresponding degree of verification was compiled. The actual scale power system is used
in the calculation. In terms of algorithm, this chapter mainly involves the approximate MIP
algorithm, expert rules algorithm, and GA-based algorithm. In terms of a model, this chapter
mainly involves the single-state model and multistate model of diagonal block matrix.

This study mainly focuses on the offline discrete reactive power optimization. It will also
consider its online application in the future. Besides the discrete reactive power optimization,
there are some other discrete optimization problems in power systems, such as generator
maintenance scheduling problems, generating unit commitment calculation, power equipment