Page 109 - Mechanical Engineers Reference Book

*

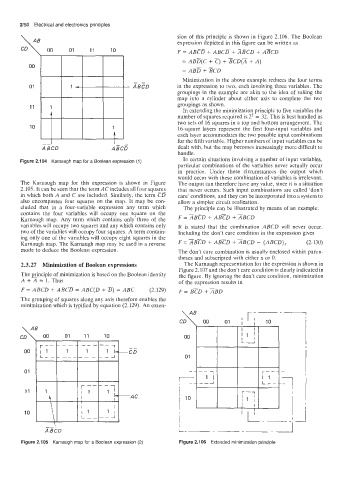
2/50 Electrical and electronics principles sion of this principle is shown in Figure 2.106. The Boolean

expression depicted in this figure can be written as
10
F=ABCD+ABCD+Z~BCD+ABCD
00
01
11
= ABD(C + E) + BCD(x + A)
00
= ABb + BCD
Minimization in the above example reduces the four terms
01 14 in the expression to two, each involving three variables. The
groupings in the example are akin to the idea of rolling the
map into a cylinder about either axis to complete the two
groupings as shown.
11 1 In extending the minimization principle to five variables the
h number of squares required is 2’ = 32. This is best handled as
two sets of 16 squares in a top and bottom arrangement. The
10 1 16-square layers represent the first four-input variables and
f each layer accommodates the two possible input combinations
for the fifth variable. Higher numbers of input variables can be
dealt with, but the map becomes increasingly more difficult to
handle.
In certain situations involving a number of input variables,
Figure 2.104 Karnaugh map for a Boolean expression (1)
particular combinations of the variables never actually occur
in practice. Under these circumstances the output which
would occur with these combination of variables is irrelevant.
The Karnaugh map for this expression is shown in Figure The output can therefore have any value, since it is a situation
2.105. It can be seen that the term ACincludes all four squaje? that never occurs. Such input combinations are called ‘don’t
in which both A and C are included. Similarly, the term CD care‘ conditions, and they can be incorporated into a system to
also encompasses four squares on the map. It may be con- allow a simpler circuit realization.
cluded that in a four-variable expression any term which The principle can be illustrated by means of an example:
contains the four variables will occupy one square on the
Karnaugh map. Any term which contains only three of the F = ABcD + ABCD + ZBCD
variables will occupy two squares and any which contains only It is stated that the combination ABCD will never occur.
two of the variables will occupy four squares. A term contain- Including the don’t care condition in the expression gives
ing only one of the variables will occupy eight squares in the
Karnaugh map. The Karnaugh map may be used in a reverse F = ZBzD + ABCD + xBCD + {ABCD}, (2.130)
mode to deduce the Boolean expression. The don‘t care combination is usually enclosed within paren-
theses and subscripted with either x or 0.
2.3.27 Minimization of Boolean expressions The Karnaugh representation for the expression is shown in
Figure 2.107 and the don’t care condition is clearly indicated in
The Kinciple of minimization is based on the Boolean identity the figure. By ignoring the don’t care condition, minimization
A + A = 1. Thus of the expression results in
F = ABCD + ABCfS = ABC(D + fS) = ABC (2.129) F = BCD + XBD
The grouping of squares along any axis therefore enables the
minimization which is typified by equation (2.129). An exten-
\ AB r----7

ABCD i-p-----p-I
Figure 2.105 Karnaugh map for a Boolean expression (2) Figure 2.106 Extended minimization principle