Page 189 - Mechanics of Asphalt Microstructure and Micromechanics

Fundamentals of Phenomenological Models 181

6.3.1.2 Creep
Under a constant stress, the phenomenon that the strain gradually increases is called
creep.
Equations 6-84a and b describe this phenomenon.
σ() = σ (6-84a)
t
0
ε() = ε + ε () (6-84b)
t
t
e c
Where s 0 represents a constant stress, e e represents the elastic strain that does not
vary with time, and e c (t) represents the creep strain that varies with time. Equation 6.85
represents the strain rate. Depending on this rate, the creep process can be divided into
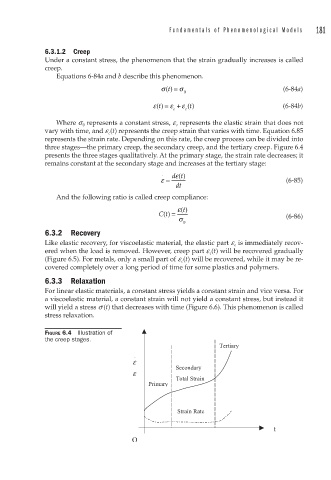
three stages—the primary creep, the secondary creep, and the tertiary creep. Figure 6.4
presents the three stages qualitatively. At the primary stage, the strain rate decreases; it
remains constant at the secondary stage and increases at the tertiary stage:
. dt
ε()
ε = (6-85)
dt
And the following ratio is called creep compliance:
ε t ()
Ct() =
σ (6-86)
0
6.3.2 Recovery
Like elastic recovery, for viscoelastic material, the elastic part e e is immediately recov-
ered when the load is removed. However, creep part e c (t) will be recovered gradually
(Figure 6.5). For metals, only a small part of e c (t) will be recovered, while it may be re-
covered completely over a long period of time for some plastics and polymers.

6.3.3 Relaxation
For linear elastic materials, a constant stress yields a constant strain and vice versa. For
a viscoelastic material, a constant strain will not yield a constant stress, but instead it
will yield a stress s (t) that decreases with time (Figure 6.6). This phenomenon is called
stress relaxation.

FIGURE 6.4 Illustration of
the creep stages.
Tertiary
.
ε
Secondary
ε
Total Strain
Primary

Strain Rate

t
O