Page 191 - Mechanics of Asphalt Microstructure and Micromechanics

Fundamentals of Phenomenological Models 183

The following ratio is called relaxation modulus:
σ t ()
Et() = (6-87)
ε
0
The above phenomena are the topics of viscoelasticity. For a mixture of AC, among
the three constituents, asphalt binder is a viscoelastic (viscoplastic) material, aggregate
is approximately an elastic material under normal loading. Due to its complex struc-
ture, in an AC specimen, creep, recovery, and relaxation may happen simultaneously,
adding the complexity of characterization and modeling.
Generally, these phenomena are a non-linear process. In future sections, the rela-
tionship between creep and relaxation will be established.

6.3.4 Linearity and Boltzmann’s Superposition Principle
If a material is considered as linearly viscoelastic, its stress is proportional to strain and
vice versa. In linear viscoelasticity, the linear superposition principle is valid. Mathe-
matically, this principle can be written in the following two equations:
εασ( )] = αεσ( )] (6-88)
t
t
[
[

−
−
εσ ( ) + σ (t t )] = εσ ( )]+ εσ (t t )]
[
[
t
t
[
1 2 1 1 2 1 (6-89)
6.3.5 Complex Loading
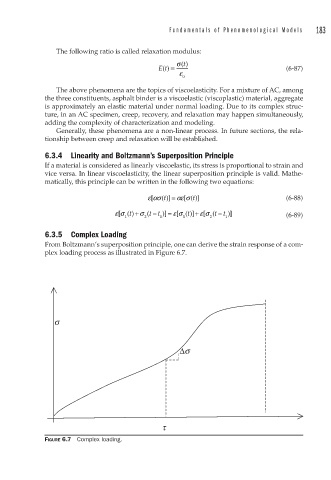
From Boltzmann’s superposition principle, one can derive the strain response of a com-
plex loading process as illustrated in Figure 6.7.

σ

Δ σ

τ

FIGURE 6.7 Complex loading.