Page 141 - Mechanics of Microelectromechanical Systems
P. 141
128 Chapter 2
Problem 2.7
A hollow trapezoid microcantilever is designed to operate in an
application where the torsion-produced tip slope is not available, and
therefore the effects of torsion have to be minimum. If the cross-section is
square and the maximum area where the trapeze can be
inscribed is a rectangle defined by and what is the best
design for this application ? Known are E = 130 GPa and
Answer:
The lengths defining the trapeze are:
and the trapeze semi-angle can range between the values of 0 to arctan
[w/(21)]. The torsional compliance is minimum for a semi-angle and
therefore for a rectangular configuration.
Problem 2.8
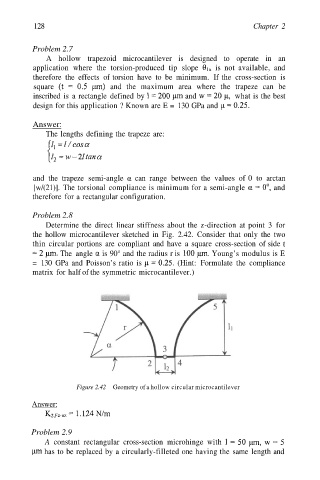
Determine the direct linear stiffness about the z-direction at point 3 for
the hollow microcantilever sketched in Fig. 2.42. Consider that only the two
thin circular portions are compliant and have a square cross-section of side
The angle is 90° and the radius r is Young’s modulus is E
= 130 GPa and Poisson’s ratio is (Hint: Formulate the compliance
matrix for half of the symmetric microcantilever.)
Figure 2.42 Geometry of a hollow circular microcantilever
Answer:
Problem 2.9
A constant rectangular cross-section microhinge with
has to be replaced by a circularly-filleted one having the same length and