Page 111 -

3.2 Theoretical Analysis 101
Table 3.6. Microspheres for analysis of solitary fiber trapping

material refractive index density (g cm −3 )radius (µm)
polystyrene 1.6 1.06 2–10
glass 1.51 2.54 2–10

0.06
Fiber end 0.04 At beam waist
Optical trapping efficiency -10 -5 -0.02 0 0.02 3 fold beam waist 10
2 fold beam waist

5

-0.04
-0.06

Off-axial distance (mm)
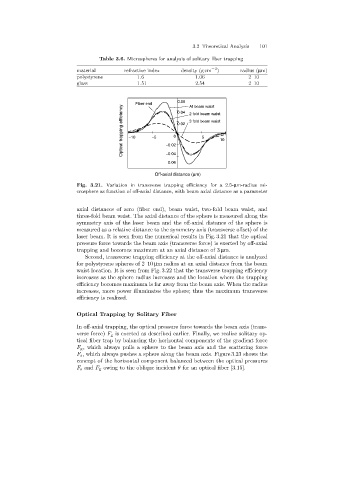
Fig. 3.21. Variation in transverse trapping efficiency for a 2.5-µm-radius mi-
crosphere as function of off-axial distance, with beam axial distance as a parameter

axial distances of zero (fiber end), beam waist, two-fold beam waist, and
three-fold beam waist. The axial distance of the sphere is measured alongthe
symmetry axis of the laser beam and the off-axial distance of the sphere is
measured as a relative distance to the symmetry axis (transverse offset) of the
laser beam. It is seen from the numerical results in Fig. 3.21 that the optical
pressure force towards the beam axis (transverse force) is exerted by off-axial
trappingand becomes maximum at an axial distance of 3 µm.
Second, transverse trappingefficiency at the off-axial distance is analyzed
for polystyrene spheres of 2–10 µm radius at an axial distance from the beam
waist location. It is seen from Fig. 3.22 that the transverse trapping efficiency
increases as the sphere radius increases and the location where the trapping
efficiency becomes maximum is far away from the beam axis. When the radius
increases, more power illuminates the sphere; thus the maximum transverse
efficiency is realized.

Optical Trapping by Solitary Fiber

In off-axial trapping, the optical pressure force towards the beam axis (trans-
verse force) F g is exerted as described earlier. Finally, we realize solitary op-
tical fiber trap by balancingthe horizontal components of the gradient force
F g , which always pulls a sphere to the beam axis and the scatteringforce
F s , which always pushes a sphere alongthe beam axis. Figure 3.23 shows the
concept of the horizontal component balanced between the optical pressures
F s and F g owingto the oblique incident θ for an optical fiber [3.15].