Page 268 - Microtectonics

260 9 · Natural Microgauges
mogeneously distributed inside the clinopyroxene crys- recrystallisation. The transition of brittle to ductile de-
tals, but at lower temperature exsolution symplectites are formation depends also on other factors (Sect. 3.14) but
formed at grain boundaries. Curved paths in tempera- mostly on strain rate; with increasing strain rate, the tem-
ture-time space can give rise to unique microstructures perature at which crystalplastic deformation starts in-
(Fig. 9.9), which can help to reconstruct P-T-t paths. Ob- creases. Nevertheless, rough guidelines can be given for
viously, such temperature gauges are most powerful when different minerals, as shown in Fig. 9.10 (Sect. 3.12).
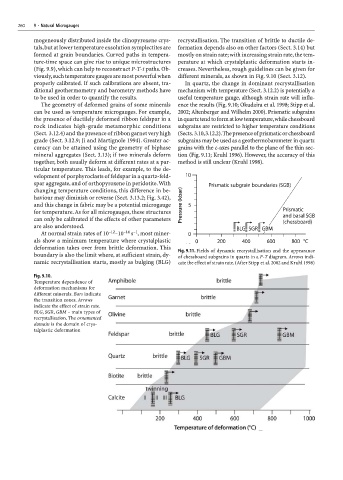
properly calibrated. If such calibrations are absent, tra- In quartz, the change in dominant recrystallisation
ditional geothermometry and barometry methods have mechanism with temperature (Sect. 3.12.2) is potentially a
to be used in order to quantify the results. useful temperature gauge, although strain rate will influ-
The geometry of deformed grains of some minerals ence the results (Fig. 9.10; Okudaira et al. 1998; Stipp et al.
can be used as temperature microgauges. For example, 2002; Altenberger and Wilhelm 2000). Prismatic subgrains
the presence of ductilely deformed ribbon feldspar in a in quartz tend to form at low temperature, while chessboard
rock indicates high-grade metamorphic conditions subgrains are restricted to higher temperature conditions
(Sect. 3.12.4) and the presence of ribbon garnet very high (Sects. 3.10, 3.12.2). The presence of prismatic or chessboard
grade (Sect. 3.12.9; Ji and Martignole 1994). Greater ac- subgrains may be used as a geothermobarometer in quartz
curacy can be attained using the geometry of biphase grains with the c-axes parallel to the plane of the thin sec-
mineral aggregates (Sect. 3.13); if two minerals deform tion (Fig. 9.11; Kruhl 1996). However, the accuracy of this
together, both usually deform at different rates at a par- method is still unclear (Kruhl 1998).
ticular temperature. This leads, for example, to the de-
velopment of porphyroclasts of feldspar in a quartz-feld-
spar aggregate, and of orthopyroxene in peridotite. With
changing temperature conditions, this difference in be-
haviour may diminish or reverse (Sect. 3.13.2; Fig. 3.42),
and this change in fabric may be a potential microgauge
for temperature. As for all microgauges, these structures
can only be calibrated if the effects of other parameters
are also understood.
s , most miner-
At normal strain rates of 10 –12 –10 –14 –1
als show a minimum temperature where crystalplastic
deformation takes over from brittle deformation. This Fig. 9.11. Fields of dynamic recrystallisation and the appearance
boundary is also the limit where, at sufficient strain, dy- of chessboard subgrains in quartz in a P-T diagram. Arrows indi-
namic recrystallisation starts, mostly as bulging (BLG) cate the effect of strain rate. (After Stipp et al. 2002 and Kruhl 1998)
Fig. 9.10.
Temperature dependence of
deformation mechanisms for
different minerals. Bars indicate
the transition zones. Arrows
indicate the effect of strain rate.
BLG, SGR, GBM – main types of
recrystallisation. The ornamented
domain is the domain of crys-
talplastic deformation